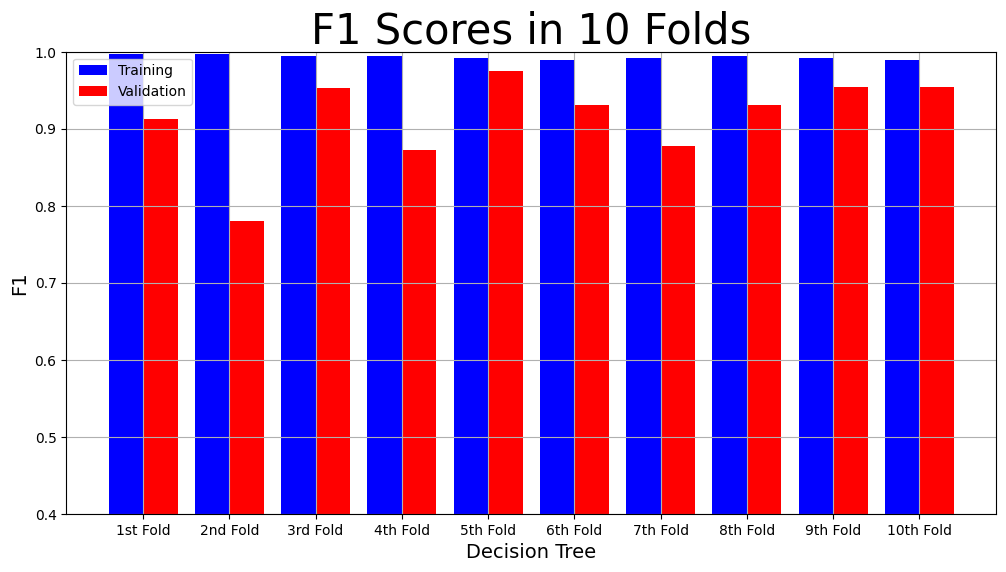
Model Fitting
Contents
Model Fitting#
# import relevant libraries
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import seaborn as sns
from sklearn.metrics import f1_score
%matplotlib inline
from google.colab import drive
drive.mount('/content/drive')
Drive already mounted at /content/drive; to attempt to forcibly remount, call drive.mount("/content/drive", force_remount=True).
From toturial: https://www.section.io/engineering-education/how-to-implement-k-fold-cross-validation/
Includes some functions I will reuse later on with our data
dataset = pd.read_csv('/content/drive/MyDrive/NMA/breast_cancer_data.csv')
# Separate features and target variable
X = dataset.iloc[:, 2:-1].values
y = dataset. iloc [:, 1].values
print("Matrix of features", X, sep='\n') # so everything except for id, and diagnosis
print("--------------------------------------------------")
print("Target Variable", y, sep='\n') #label diagnosis
Matrix of features
[[1.799e+01 1.038e+01 1.228e+02 ... 2.654e-01 4.601e-01 1.189e-01]
[2.057e+01 1.777e+01 1.329e+02 ... 1.860e-01 2.750e-01 8.902e-02]
[1.969e+01 2.125e+01 1.300e+02 ... 2.430e-01 3.613e-01 8.758e-02]
...
[1.660e+01 2.808e+01 1.083e+02 ... 1.418e-01 2.218e-01 7.820e-02]
[2.060e+01 2.933e+01 1.401e+02 ... 2.650e-01 4.087e-01 1.240e-01]
[7.760e+00 2.454e+01 4.792e+01 ... 0.000e+00 2.871e-01 7.039e-02]]
--------------------------------------------------
Target Variable
['M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M'
'M' 'B' 'B' 'B' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M'
'M' 'B' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'M'
'M' 'B' 'M' 'M' 'B' 'B' 'B' 'B' 'M' 'B' 'M' 'M' 'B' 'B' 'B' 'B' 'M' 'B'
'M' 'M' 'B' 'M' 'B' 'M' 'M' 'B' 'B' 'B' 'M' 'M' 'B' 'M' 'M' 'M' 'B' 'B'
'B' 'M' 'B' 'B' 'M' 'M' 'B' 'B' 'B' 'M' 'M' 'B' 'B' 'B' 'B' 'M' 'B' 'B'
'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'M' 'M' 'B' 'M' 'M' 'B' 'B' 'B'
'M' 'M' 'B' 'M' 'B' 'M' 'M' 'B' 'M' 'M' 'B' 'B' 'M' 'B' 'B' 'M' 'B' 'B'
'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'M'
'M' 'B' 'M' 'B' 'B' 'M' 'M' 'B' 'B' 'M' 'M' 'B' 'B' 'B' 'B' 'M' 'B' 'B'
'M' 'M' 'M' 'B' 'M' 'B' 'M' 'B' 'B' 'B' 'M' 'B' 'B' 'M' 'M' 'B' 'M' 'M'
'M' 'M' 'B' 'M' 'M' 'M' 'B' 'M' 'B' 'M' 'B' 'B' 'M' 'B' 'M' 'M' 'M' 'M'
'B' 'B' 'M' 'M' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'M' 'M' 'B' 'B' 'M'
'B' 'B' 'M' 'M' 'B' 'M' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'M' 'B'
'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'M' 'B' 'B' 'B' 'B'
'B' 'B' 'M' 'B' 'M' 'B' 'B' 'M' 'B' 'B' 'M' 'B' 'M' 'M' 'B' 'B' 'B' 'B'
'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'M' 'B' 'M' 'B' 'B' 'B'
'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'M' 'B' 'M'
'B' 'B' 'B' 'B' 'M' 'M' 'M' 'B' 'B' 'B' 'B' 'M' 'B' 'M' 'B' 'M' 'B' 'B'
'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'M' 'M' 'B' 'B' 'B' 'B' 'B' 'B'
'B' 'B' 'B' 'B' 'B' 'M' 'M' 'B' 'M' 'M' 'M' 'B' 'M' 'M' 'B' 'B' 'B' 'B'
'B' 'M' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'M' 'B' 'B' 'M' 'M' 'B' 'B'
'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B'
'M' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B'
'M' 'M' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'M' 'B' 'M' 'B' 'B' 'M'
'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'M' 'B' 'B' 'B' 'B' 'B' 'B'
'M' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'B'
'B' 'M' 'B' 'M' 'B' 'B' 'M' 'B' 'B' 'B' 'B' 'B' 'M' 'M' 'B' 'M' 'B' 'M'
'B' 'B' 'B' 'B' 'B' 'M' 'B' 'B' 'M' 'B' 'M' 'B' 'M' 'M' 'B' 'B' 'B' 'M'
'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'M' 'B' 'M' 'M' 'B' 'B' 'B'
'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B' 'B'
'B' 'B' 'B' 'B' 'M' 'M' 'M' 'M' 'M' 'M' 'B']
# Label Encode the target variable
# Change target variable to numerical values
# The number 0 represents benign, while 1 represents malignant.
from sklearn.preprocessing import LabelEncoder
label_encoder = LabelEncoder()
encoded_y = label_encoder.fit_transform(y)
label_encoder_name_mapping = dict(zip(label_encoder.classes_,
label_encoder.transform(label_encoder.classes_)))
print("Mapping of Label Encoded Classes", label_encoder_name_mapping, sep="\n")
print("Label Encoded Target Variable", encoded_y, sep="\n")
Mapping of Label Encoded Classes
{'B': 0, 'M': 1}
Label Encoded Target Variable
[1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 0 0 0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
0 1 1 1 1 1 1 1 1 0 1 0 0 0 0 0 1 1 0 1 1 0 0 0 0 1 0 1 1 0 0 0 0 1 0 1 1
0 1 0 1 1 0 0 0 1 1 0 1 1 1 0 0 0 1 0 0 1 1 0 0 0 1 1 0 0 0 0 1 0 0 1 0 0
0 0 0 0 0 0 1 1 1 0 1 1 0 0 0 1 1 0 1 0 1 1 0 1 1 0 0 1 0 0 1 0 0 0 0 1 0
0 0 0 0 0 0 0 0 1 0 0 0 0 1 1 0 1 0 0 1 1 0 0 1 1 0 0 0 0 1 0 0 1 1 1 0 1
0 1 0 0 0 1 0 0 1 1 0 1 1 1 1 0 1 1 1 0 1 0 1 0 0 1 0 1 1 1 1 0 0 1 1 0 0
0 1 0 0 0 0 0 1 1 0 0 1 0 0 1 1 0 1 0 0 0 0 1 0 0 0 0 0 1 0 1 1 1 1 1 1 1
1 1 1 1 1 1 1 0 0 0 0 0 0 1 0 1 0 0 1 0 0 1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0
0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 1 0 0 0 1 0 1 0 0 0 0 1 1 1 0 0
0 0 1 0 1 0 1 0 0 0 1 0 0 0 0 0 0 0 1 1 1 0 0 0 0 0 0 0 0 0 0 0 1 1 0 1 1
1 0 1 1 0 0 0 0 0 1 0 0 0 0 0 1 0 0 0 1 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0
0 1 0 0 0 0 0 1 0 0 1 0 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 1 0 0 0 0 0 1 0 0
1 0 1 0 0 1 0 1 0 0 0 0 0 0 0 0 1 1 0 0 0 0 0 0 1 0 0 0 0 0 0 0 0 0 0 1 0
0 0 0 0 0 0 1 0 1 0 0 1 0 0 0 0 0 1 1 0 1 0 1 0 0 0 0 0 1 0 0 1 0 1 0 1 1
0 0 0 1 0 0 0 0 0 0 0 0 0 0 0 1 0 1 1 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 1 1 1 1 1 0]
# from sklearn.tree import DecisionTreeClassifier
# #define the model
# decision_tree_model = DecisionTreeClassifier(criterion="entropy",
# random_state=0)
# #perform cross validation with model
# decision_tree_result = cross_validation(decision_tree_model, X, encoded_y, 10)
# print(decision_tree_result)
# # Plot Accuracy Result
# model_name = "Decision Tree"
# plot_result(model_name,
# "Accuracy",
# "Accuracy scores in 10 Folds",
# decision_tree_result["Training Accuracy scores"],
# decision_tree_result["Validation Accuracy scores"])
Model fMRI#
# load dataset
data_BOLD = pd.read_csv('/content/drive/MyDrive/NMA/BOLD_contrast_network_98.csv')
data_IES = pd.read_csv('/content/drive/MyDrive/NMA/ies_scores_98.csv')
data_personality = pd.read_csv('/content/drive/MyDrive/NMA/median_personality _98.csv')
data_IES
| SUBJECTS | EMOTION T1 IES | EMOTION T2 IES | SOCIAL T1 IES | SOCIAL T2 IES | GAMBLING IES | |
|---|---|---|---|---|---|---|
| 0 | 100307 | 6.994464 | 6.238000 | 4.790000 | 5.750 | 3.609062 |
| 1 | 100408 | 7.119444 | 6.708667 | 10.593333 | 12.675 | 4.811875 |
| 2 | 101915 | 9.155087 | 8.345333 | 11.930000 | 13.990 | 5.093125 |
| 3 | 102816 | 7.111111 | 6.612000 | 11.890000 | 14.195 | 4.874375 |
| 4 | 103414 | 7.847222 | 8.561333 | 7.386667 | 7.955 | 4.704063 |
| ... | ... | ... | ... | ... | ... | ... |
| 93 | 199655 | 7.082907 | 6.660000 | 6.656667 | 9.225 | 3.010625 |
| 94 | 200614 | 7.932778 | 8.359333 | 6.043333 | 8.830 | 4.212500 |
| 95 | 201111 | 11.040556 | 9.281333 | 10.126667 | 10.270 | 5.563750 |
| 96 | 201414 | 8.061667 | 8.048000 | 9.090000 | 11.725 | 3.100312 |
| 97 | 205119 | 8.516055 | 7.414000 | 7.970000 | 21.400 | 5.100937 |
98 rows × 6 columns
data_BOLD
| subject_id | Emotion_Auditory_L | Emotion_Auditory_R | Emotion_Cingulo-Oper_L | Emotion_Cingulo-Oper_R | Emotion_Default_L | Emotion_Default_R | Emotion_Dorsal-atten_L | Emotion_Dorsal-atten_R | Emotion_Frontopariet_L | ... | Gambling_Posterior-Mu_L | Gambling_Posterior-Mu_R | Gambling_Somatomotor_L | Gambling_Somatomotor_R | Gambling_Ventral-Mult_L | Gambling_Ventral-Mult_R | Gambling_Visual1_L | Gambling_Visual1_R | Gambling_Visual2_L | Gambling_Visual2_L.1 | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 100307 | -2.804921 | -2.433804 | -0.777985 | -0.353353 | 10.053771 | 5.986613 | 11.420777 | 8.673832 | 4.628537 | ... | -7.973004 | 2.530932 | -3.179724 | -1.810594 | -7.124124 | 1.524933 | -3.339643 | -3.025932 | 8.826484 | 7.199637 |
| 1 | 100408 | 3.516186 | 7.529671 | -9.521039 | -5.284645 | -8.731886 | 7.884268 | 11.791724 | 1.867515 | -8.937923 | ... | -24.315753 | -18.506888 | -6.057032 | 4.568156 | -48.646206 | -11.067792 | -16.796800 | -5.983401 | -8.297101 | 6.657371 |
| 2 | 101915 | 9.980518 | 5.266869 | 9.546204 | 11.319655 | 8.908589 | 20.103598 | 0.907064 | 12.911264 | 2.576694 | ... | -1.944254 | -0.950986 | 0.150241 | 3.160913 | -8.325856 | -9.110250 | -7.625908 | -1.689586 | -1.384789 | 1.175621 |
| 3 | 102816 | 20.833271 | -16.487274 | 1.886792 | -0.946059 | 10.643481 | 3.247931 | 13.517639 | 13.682730 | -7.682030 | ... | -3.673315 | -2.800902 | 12.236763 | 6.242775 | -9.369718 | -12.720637 | 8.636415 | 20.621203 | 9.931208 | 8.350895 |
| 4 | 103414 | 9.885700 | 5.633930 | 9.734162 | 9.824339 | 13.819462 | 21.356125 | 21.945681 | 7.596248 | 13.637148 | ... | 9.498112 | 7.589702 | 4.858379 | 14.831399 | 21.459354 | -7.949689 | 18.820264 | 10.545901 | 12.616854 | 12.111169 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 93 | 199655 | -3.796242 | -3.248363 | -12.931731 | -7.968932 | -1.838899 | -2.248285 | -0.109514 | 1.404556 | -8.534893 | ... | -4.010796 | 1.193511 | 0.801685 | -0.544744 | -0.791156 | 22.397713 | -2.309791 | 9.854299 | -1.874123 | 0.729667 |
| 94 | 200614 | -2.340933 | -0.460370 | -6.904875 | -13.213405 | -0.929012 | -7.979797 | 11.367749 | 18.012441 | -1.613193 | ... | 11.388163 | 11.611773 | -12.670486 | 4.437090 | 1.793672 | -0.470018 | -8.310730 | 9.031029 | -6.830466 | -0.281131 |
| 95 | 201111 | -0.313696 | -3.006372 | 7.014663 | -1.106524 | 7.094315 | 1.009450 | 9.850395 | 6.223135 | 2.587723 | ... | -1.079248 | 10.458447 | -10.125810 | -8.503565 | 6.909634 | 26.248419 | 15.927485 | 13.441762 | 6.393254 | 4.603233 |
| 96 | 201414 | 9.047621 | 3.032789 | -4.672088 | -2.014852 | 0.149621 | 22.042231 | 1.823159 | 22.238250 | -1.161439 | ... | 4.350870 | 2.288127 | -0.454990 | 7.512785 | 10.580950 | 7.709618 | 0.995246 | 0.200687 | 3.556047 | 14.316392 |
| 97 | 205119 | 18.881525 | 12.401503 | 7.964594 | -0.326323 | 24.005220 | 15.183962 | 16.718064 | 9.807230 | 15.608610 | ... | -15.698724 | -16.134373 | -19.458602 | -16.554394 | -16.920817 | -41.737430 | 14.800047 | 19.709679 | -5.829851 | -10.290764 |
98 rows × 73 columns
data_IES
| SUBJECTS | EMOTION T1 IES | EMOTION T2 IES | SOCIAL T1 IES | SOCIAL T2 IES | GAMBLING IES | |
|---|---|---|---|---|---|---|
| 0 | 100307 | 6.994464 | 6.238000 | 4.790000 | 5.750 | 3.609062 |
| 1 | 100408 | 7.119444 | 6.708667 | 10.593333 | 12.675 | 4.811875 |
| 2 | 101915 | 9.155087 | 8.345333 | 11.930000 | 13.990 | 5.093125 |
| 3 | 102816 | 7.111111 | 6.612000 | 11.890000 | 14.195 | 4.874375 |
| 4 | 103414 | 7.847222 | 8.561333 | 7.386667 | 7.955 | 4.704063 |
| ... | ... | ... | ... | ... | ... | ... |
| 93 | 199655 | 7.082907 | 6.660000 | 6.656667 | 9.225 | 3.010625 |
| 94 | 200614 | 7.932778 | 8.359333 | 6.043333 | 8.830 | 4.212500 |
| 95 | 201111 | 11.040556 | 9.281333 | 10.126667 | 10.270 | 5.563750 |
| 96 | 201414 | 8.061667 | 8.048000 | 9.090000 | 11.725 | 3.100312 |
| 97 | 205119 | 8.516055 | 7.414000 | 7.970000 | 21.400 | 5.100937 |
98 rows × 6 columns
data_personality
| Subject | NEOFAC_A | NEOFAC_O | NEOFAC_C | NEOFAC_N | NEOFAC_E | |
|---|---|---|---|---|---|---|
| 0 | 100307 | 1 | 0 | 1 | 0 | 1 |
| 1 | 100408 | 0 | 1 | 0 | 0 | 1 |
| 2 | 101915 | 1 | 1 | 1 | 0 | 1 |
| 3 | 102816 | 1 | 0 | 0 | 0 | 1 |
| 4 | 103414 | 0 | 1 | 0 | 1 | 1 |
| ... | ... | ... | ... | ... | ... | ... |
| 93 | 199655 | 0 | 1 | 0 | 0 | 0 |
| 94 | 200614 | 1 | 0 | 1 | 0 | 1 |
| 95 | 201111 | 1 | 1 | 1 | 1 | 0 |
| 96 | 201414 | 1 | 1 | 1 | 0 | 1 |
| 97 | 205119 | 1 | 1 | 1 | 0 | 1 |
98 rows × 6 columns
# Format features and target variable
X_IES = data_IES.iloc[:, 1:].values
X_BOLD = data_BOLD.iloc[:,1:].values
#personality
y_A = data_personality.iloc[:, 1].values
y_O = data_personality.iloc[:, 2].values
y_C = data_personality.iloc[:, 3].values
y_N = data_personality.iloc[:, 4].values
y_E = data_personality.iloc[:, 5].values
print("Matrix of features", X_IES, sep='\n') # so everything except for id, and diagnosis
print("--------------------------------------------------")
print("Matrix of features BOLD", X_BOLD, sep='\n') # so everything except for id, and diagnosis
print("--------------------------------------------------")
print("Target Variable", y_A, sep='\n') #label Agreeableness
Matrix of features
[[ 6.99446367 6.238 4.79 5.75 3.6090625 ]
[ 7.11944444 6.70866667 10.59333333 12.675 4.811875 ]
[ 9.1550865 8.34533333 11.93 13.99 5.093125 ]
[ 7.11111111 6.612 11.89 14.195 4.874375 ]
[ 7.84722222 8.56133333 7.38666667 7.955 4.7040625 ]
[ 7.71722222 8.13520408 10.8075 21.38 3.329375 ]
[ 9.17555556 7.97066667 9.14 19.8 3.678125 ]
[ 7.55944444 7.17 9.14 15.1 3.555 ]
[ 6.64945312 7.00533333 7.12666667 6.49 3.0796875 ]
[ 7.855 7.23333333 6.80333333 7.095 3.3903125 ]
[ 7.65404844 8.12933333 11.81666667 12.22 8.1771875 ]
[ 8.25444444 10.50532544 8.62 7.605 3.0190625 ]
[ 6.98777778 8.168 11.48666667 10.125 3.63625 ]
[ 8.356609 6.99933333 5.24666667 33.92 3.7440625 ]
[ 7.38222222 7.73133333 7.76666667 8.095 2.980625 ]
[ 7.86833333 8.65866667 6.83 18.53 5.8440625 ]
[ 5.87647059 5.23266667 23.91 9.3 3.91225807]
[ 9.01722222 9.51666667 9.39666667 11.51 4.42006244]
[ 7.38722222 7.872 10.575 6.955 3.9453125 ]
[ 8.4 8.974 5.91 7.23 6.2940625 ]
[ 7.97888889 8.86533333 8.27333333 8.44 5.06305931]
[ 8.61611111 9.432 7.07 9.84 5.6909375 ]
[ 7.77888889 8.34030612 8.56666667 6.88 3.14 ]
[ 7.10555556 6.52466667 6.58666667 10.725 5.16795005]
[10.22695312 7.456 8.65666667 15.24 5.880625 ]
[ 7.51833333 8.72133333 9.84 11.975 6.27080125]
[ 7.51666667 6.96 8.49333333 6.425 5.4365625 ]
[10.88666667 10.89413265 10.58 8.57 5.219375 ]
[ 7.19333333 9.21733333 4.57666667 4.665 2.9871875 ]
[ 8.195 5.778 8.33 7.76 4.95983351]
[ 8.735 9.04733333 37.65 18.02 5.125625 ]
[ 6.09 6.14533333 8.06 9.36 2.6371875 ]
[ 8.40456747 8.47066667 7.67666667 22.64 4.2840625 ]
[ 6.41777778 6.60266667 7.62333333 12.02 6.8284375 ]
[ 9.34111111 8.94066667 8.56333333 15.03 5.77125 ]
[ 8.95722222 8.86666667 7.89666667 7.27 2.46875 ]
[ 7.07979239 5.518 7.07333333 10.445 2.4490625 ]
[ 5.46 6.12333333 6.05 6.195 3.4141103 ]
[ 7.49722222 6.256 6.47 6.235 4.2884375 ]
[ 9.08333333 8.956 7.97666667 6.385 3.6946875 ]
[ 8.38611111 8.17266667 9.88333333 4.585 6.61125 ]
[ 9.00351563 9.26709184 9.91 15.18 2.85502601]
[ 9.58833333 11.01333333 8.1975 5.765 2.980625 ]
[ 8.60388889 7.69533333 9.66333333 11.425 3.8365625 ]
[ 7.28888889 7.11333333 5.78666667 6.445 3.7728125 ]
[ 8.77944444 8.74438775 10.9575 11.23 4.10375 ]
[ 7.52013841 7.438 5.57333333 10.04 3.84375 ]
[ 7.94722222 7.25466667 7.42 6.54 3.84099896]
[ 8.73716263 10.753125 7.02666667 14.4 3.721875 ]
[ 7.00888889 7.46933333 9.12 7.135 3.68316337]
[ 9.95666667 10.5408284 10.22 29.34 5.5071875 ]
[ 7.85522491 6.63266667 7.44333333 10.12 3.68375 ]
[ 7.56666667 7.95933333 10.86 14.12 3.7296875 ]
[ 7.01388889 7.472 12.04333333 12.745 4.6921875 ]
[ 5.91010381 5.73466667 21.41666667 26.76 5.94125 ]
[ 8.935 8.378 14.58333333 21.96 5.76899063]
[ 6.95 7.96530612 7.59333333 8.915 3.7725 ]
[ 7.60944444 10.75255102 10.31333333 10.2 3.7203125 ]
[ 6.78277778 6.03866667 5.49666667 6.905 3.2825 ]
[ 6.00444444 6.81733333 6.47 5.43 4.596875 ]
[ 6.30611111 6.89133333 9.26333333 6.96 4.6284375 ]
[ 8.025 7.47466667 8.41333333 7.205 3.79338189]
[ 9.17555556 8.728 11.3475 8.37 4.7103125 ]
[ 9.30269896 10.14266667 13.67666667 24.94 4.845625 ]
[ 7.13055556 7.752 5.55333333 5.56 3.1428125 ]
[ 8.3983391 6.92866667 5.73333333 5.995 3.633125 ]
[ 9.705 9.826 10.01666667 6.005 5.4121875 ]
[10.5032 8.246 7.06666667 8.72 4.22625 ]
[10.22222222 8.90066667 5.43333333 6.82 3.4578125 ]
[ 7.98555556 8.29066667 8.565 7.28 3.6975 ]
[ 7.12588235 6.42866667 6.62 6.1 4.195625 ]
[ 9.32222222 9.08666667 7.59666667 5.81 4.4125 ]
[ 8.04444444 8.57 13.13 12.23 4.7103125 ]
[ 5.94055556 5.76533333 6.94 6.16 4.3484375 ]
[ 6.85277778 6.24533333 8.18333333 8.515 4.226875 ]
[ 8.24055556 7.894 10.02333333 11.74 4.76906667]
[ 9.53833333 8.56333333 9.40666667 7.685 4.43125 ]
[ 9.36277778 10.12866667 6.20666667 6.25 5.1765625 ]
[ 7.83965398 6.996 16.3575 11.815 5.125 ]
[ 7.79222222 10.72333333 9.18666667 10.67 4.8859375 ]
[ 8.155 8.492 7.87 25.7 3.4203125 ]
[ 7.58242214 7.282 8.19666667 9.025 4.8871875 ]
[ 6.75111111 7.84438775 13.65 7.93 4.51629553]
[ 7.97888889 8.686 7.38333333 6.115 3.34875 ]
[ 7.77722222 6.66733333 7.54 13.4 4.825 ]
[ 9.79555556 9.48333333 7.86666667 8.865 5.075 ]
[ 9.11444444 8.40133333 6.18333333 13.85 5.2553125 ]
[ 6.94888889 6.344 8.36 13.88 4.35 ]
[ 7.83333333 8.22666667 21.5175 20.92 3.8226847 ]
[ 6.59777778 7.18010204 11.73 5.8 3.8321875 ]
[ 7.09055556 7.49 7.06666667 28.98 3.1084375 ]
[ 7.72567474 7.476 8.02333333 8.58 4.6753125 ]
[ 8.06166667 7.386 5.05333333 5.33 3.450625 ]
[ 7.08290657 6.66 6.65666667 9.225 3.010625 ]
[ 7.93277778 8.35933333 6.04333333 8.83 4.2125 ]
[11.04055556 9.28133333 10.12666667 10.27 5.56375 ]
[ 8.06166667 8.048 9.09 11.725 3.1003125 ]
[ 8.51605536 7.414 7.97 21.4 5.1009375 ]]
--------------------------------------------------
Matrix of features BOLD
[[ -2.80492079 -2.43380419 -0.77798455 ... -3.0259323 8.82648362
7.19963736]
[ 3.5161865 7.52967116 -9.52103931 ... -5.98340103 -8.29710147
6.65737091]
[ 9.9805183 5.266869 9.54620418 ... -1.68958553 -1.38478885
1.17562126]
...
[ -0.31369563 -3.00637191 7.01466318 ... 13.44176231 6.39325368
4.60323275]
[ 9.04762062 3.0327889 -4.67208768 ... 0.20068705 3.5560471
14.31639195]
[ 18.88152454 12.40150292 7.9645944 ... 19.7096792 -5.82985081
-10.29076429]]
--------------------------------------------------
Target Variable
[1 0 1 1 0 0 1 1 0 1 1 0 1 0 0 0 1 1 0 1 0 1 0 0 0 1 0 0 0 0 1 1 0 1 1 0 0
1 0 0 1 0 1 1 1 0 1 1 0 0 0 1 0 1 0 0 0 0 0 0 0 1 0 0 1 1 1 1 1 0 1 1 1 1
1 0 1 0 0 0 1 1 0 0 1 1 1 1 0 0 1 0 1 0 1 1 1 1]
Let’s analyze the data first
from collections import Counter
print(dict(Counter(y_A))) #Agreeableness
print(dict(Counter(y_O))) #Openness
print(dict(Counter(y_C))) #Conscientiousness
print(dict(Counter(y_N))) #Neuroticism
print(dict(Counter(y_E))) #Extraversion
{1: 50, 0: 48}
{0: 48, 1: 50}
{1: 52, 0: 46}
{0: 46, 1: 52}
{1: 51, 0: 47}
In y_A, y_O,and y_C, there is only one element with label 0. This makes it impossible to train a model using label 0 and also evaluate it on that label.
The data is now well distributed
Functions to train the model#
Training y_N (Please ignore)
# make a copy to keep the original data without labels
data_BOLD_ye = data_BOLD.copy()
data_BOLD_ye['y_E'] = y_E
# data_BOLD_ye_clean = data_BOLD_ye[data_BOLD_ye['y_E'] != 0]
X_BOLD_ye = data_BOLD_ye.iloc[:,1:-1].values # does not include subject_id and y_E
bold_y_E = data_BOLD_ye['y_E'].values
# make a copy to keep the original data without labels
data_IES_ye = data_IES.copy()
data_IES_ye['y_E'] = y_E
data_IES_ye_clean = data_IES_ye[data_IES_ye['y_E'] != 0]
X_IES_ye = data_IES_ye_clean.iloc[:,1:-1].values # does not include subject_id and y_E
ies_y_E = data_IES_ye_clean['y_E'].values
#since the values of y_E are '1' and '2'. I will do -1 to each element to get '0' and '1'
ies_y_E = ies_y_E-1
y_N
# make a copy to keep the original data without labels
data_BOLD_yn = data_BOLD.copy()
data_BOLD_yn['y_N'] = y_N
data_BOLD_yn_clean = data_BOLD_yn[data_BOLD_yn['y_N'] != 2]
X_BOLD_yn = data_BOLD_yn_clean.iloc[:,1:-1].values # does not include subject_id and y_N
bold_y_N = data_BOLD_yn_clean['y_N'].values
# make a copy to keep the original data without labels
data_IES_yn = data_IES.copy()
data_IES_yn['y_N'] = y_N
data_IES_yn_clean = data_IES_yn[data_IES_yn['y_N'] != 2] #outlier class is 2
X_IES_yn = data_IES_yn_clean.iloc[:,1:-1].values # does not include subject_id and y_N
ies_y_N = data_IES_yn_clean['y_N'].values
y_A
dict(Counter(y_A))
{1: 50, 0: 48}
# make a copy to keep the original data without labels
data_BOLD_ya = data_BOLD.copy()
data_BOLD_ya['y_A'] = y_A
data_BOLD_ya_clean = data_BOLD_ya[data_BOLD_ya['y_A'] != 0]
data_BOLD_ya1_clean = data_BOLD_ya_clean[data_BOLD_ya_clean['y_A'] == 1]
# add repeated data points with label 1 to oversample this class and make the dataset balanced
data_BOLD_ya_clean = pd.concat([data_BOLD_ya_clean, data_BOLD_ya1_clean])
data_BOLD_ya_clean = data_BOLD_ya_clean.sample(frac=1, random_state=42)
X_BOLD_ya = data_BOLD_ya_clean.iloc[:,1:-1].values # does not include subject_id and y_A
bold_y_A = data_BOLD_ya_clean['y_A'].values
#since the values of y_A are '1' and '2'. I will do -1 to each element to get '0' and '1'
bold_y_A = bold_y_A-1
dict(Counter(bold_y_A))
{0: 100}
# make a copy to keep the original data without labels
data_IES_ya = data_IES.copy()
data_IES_ya['y_A'] = y_A
data_IES_ya_clean = data_IES_ya[data_IES_ya['y_A'] != 0]
data_IES_ya1_clean = data_IES_ya[data_IES_ya['y_A'] == 1]
# add repeated data points with label 1 to oversample this class and make the dataset balanced
data_IES_ya_clean = pd.concat([data_IES_ya_clean, data_IES_ya1_clean])
X_IES_ya = data_IES_ya_clean.iloc[:,1:-1].values # does not include subject_id and y_A
ies_y_A = data_IES_ya_clean['y_A'].values
#since the values of y_A are '1' and '2'. I will do -1 to each element to get '0' and '1'
ies_y_A = ies_y_A-1
Extract relevant network#
#Extract relevant network
# Social Cognition: dorso-atten, cingulo oper, default network
# Gambling: Cingulo-Oper, Somatomotor
# Emotion: Posterior-Mu, Orbito-Affec
list_rel_networks = ["Emotion_Orbito-Affec_L" , "Emotion_Orbito-Affec_R" , "Emotion_Posterior-Mu_L" , "Emotion_Posterior-Mu_R",
"Social_Default_L" , "Social_Default_R" , "Social_Dorsal-atten_L" , "Social_Dorsal-atten_R" , "Social_Cingulo-Oper_L" , "Social_Cingulo-Oper_R",
"Gambling_Cingulo-Oper_L" , "Gambling_Cingulo-Oper_R","Gambling_Somatomotor_L","Gambling_Somatomotor_R"]
data_BOLD_rel_networks = data_BOLD.loc[:, list_rel_networks]
X_BOLD_rel_networks = data_BOLD.loc[:, list_rel_networks].values
print("X_BOLD_rel",X_BOLD_rel_networks)
data_BOLD_rel_networks
X_BOLD_rel [[ 28.43122907 0.45423503 5.57731995 ... -2.72906399 -3.17972421
-1.81059444]
[ -2.28557407 10.50433129 3.48441709 ... 1.55804715 -6.05703247
4.56815643]
[ 2.37558422 20.70941068 10.91275624 ... 7.90590405 0.1502409
3.16091272]
...
[ 6.09024801 7.16814804 2.71281271 ... -16.94888299 -10.12580988
-8.50356458]
[ 20.06966877 -2.22965354 1.99569376 ... 11.16623543 -0.45498965
7.51278519]
[ 20.63729181 21.44628432 20.10109145 ... -13.64763183 -19.45860156
-16.55439367]]
| Emotion_Orbito-Affec_L | Emotion_Orbito-Affec_R | Emotion_Posterior-Mu_L | Emotion_Posterior-Mu_R | Social_Default_L | Social_Default_R | Social_Dorsal-atten_L | Social_Dorsal-atten_R | Social_Cingulo-Oper_L | Social_Cingulo-Oper_R | Gambling_Cingulo-Oper_L | Gambling_Cingulo-Oper_R | Gambling_Somatomotor_L | Gambling_Somatomotor_R | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0 | 28.431229 | 0.454235 | 5.577320 | -2.292669 | 7.947511 | 9.692712 | 7.256165 | 7.648978 | 2.103778 | -4.409611 | 0.201830 | -2.729064 | -3.179724 | -1.810594 |
| 1 | -2.285574 | 10.504331 | 3.484417 | 6.491784 | 1.251033 | 23.132281 | 17.014608 | 13.279836 | 3.523961 | 11.183352 | -10.916530 | 1.558047 | -6.057032 | 4.568156 |
| 2 | 2.375584 | 20.709411 | 10.912756 | 14.266931 | 3.360379 | 26.191055 | 11.821487 | 4.827629 | -6.936404 | 2.386275 | 6.541618 | 7.905904 | 0.150241 | 3.160913 |
| 3 | -6.299961 | 11.344551 | -16.024109 | -6.153889 | 31.087654 | 43.157114 | 33.487436 | 9.643869 | 39.793509 | 21.317714 | 15.593201 | 4.404389 | 12.236763 | 6.242775 |
| 4 | 21.917341 | -9.262694 | 10.743872 | 6.427080 | 24.837916 | 16.653878 | 16.779754 | 0.681534 | 13.613428 | 0.102399 | 1.520076 | 8.167790 | 4.858379 | 14.831399 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 93 | 2.353674 | -5.315302 | -2.678669 | -3.597959 | 6.386875 | 15.979174 | 9.778716 | 16.583812 | 1.405442 | 1.693786 | 3.011257 | -0.583554 | 0.801685 | -0.544744 |
| 94 | 13.488223 | -2.153168 | -0.915092 | -11.025394 | 6.462592 | 20.029918 | 12.159982 | 28.898447 | 0.610042 | 2.912552 | -3.312991 | 5.908460 | -12.670486 | 4.437090 |
| 95 | 6.090248 | 7.168148 | 2.712813 | 1.874720 | 0.794011 | 13.211028 | 5.884091 | 9.997345 | -16.163660 | -13.464351 | -15.076135 | -16.948883 | -10.125810 | -8.503565 |
| 96 | 20.069669 | -2.229654 | 1.995694 | 12.395959 | -14.147689 | 21.109725 | 16.930378 | 0.463004 | -4.729206 | -11.472062 | 11.540953 | 11.166235 | -0.454990 | 7.512785 |
| 97 | 20.637292 | 21.446284 | 20.101091 | 18.260701 | 12.243844 | -18.868113 | 13.676068 | -25.399274 | 15.839693 | -18.173780 | -24.940111 | -13.647632 | -19.458602 | -16.554394 |
98 rows × 14 columns
Merging data for model 1.2 and 2.2#
# wanna merge X_IES with X_BOLD_rel_network
# maybe row extend??
df_all = pd.concat([data_IES, data_BOLD_rel_networks.iloc[:, 1:]], axis=1)
X_combined = df_all.iloc[:, 1:].values
# print(df_all)
print(X_combined)
[[ 6.99446367 6.238 4.79 ... -2.72906399 -3.17972421
-1.81059444]
[ 7.11944444 6.70866667 10.59333333 ... 1.55804715 -6.05703247
4.56815643]
[ 9.1550865 8.34533333 11.93 ... 7.90590405 0.1502409
3.16091272]
...
[ 11.04055556 9.28133333 10.12666667 ... -16.94888299 -10.12580988
-8.50356458]
[ 8.06166667 8.048 9.09 ... 11.16623543 -0.45498965
7.51278519]
[ 8.51605536 7.414 7.97 ... -13.64763183 -19.45860156
-16.55439367]]
df_allnets = pd.concat([data_IES, data_BOLD.iloc[:, 1:]], axis=1)
X_combined_all = df_allnets.iloc[:, 1:].values
print(df_allnets)
print(X_combined_all)
SUBJECTS EMOTION T1 IES EMOTION T2 IES SOCIAL T1 IES SOCIAL T2 IES \
0 100307 6.994464 6.238000 4.790000 5.750
1 100408 7.119444 6.708667 10.593333 12.675
2 101915 9.155087 8.345333 11.930000 13.990
3 102816 7.111111 6.612000 11.890000 14.195
4 103414 7.847222 8.561333 7.386667 7.955
.. ... ... ... ... ...
93 199655 7.082907 6.660000 6.656667 9.225
94 200614 7.932778 8.359333 6.043333 8.830
95 201111 11.040556 9.281333 10.126667 10.270
96 201414 8.061667 8.048000 9.090000 11.725
97 205119 8.516055 7.414000 7.970000 21.400
GAMBLING IES Emotion_Auditory_L Emotion_Auditory_R \
0 3.609062 -2.804921 -2.433804
1 4.811875 3.516186 7.529671
2 5.093125 9.980518 5.266869
3 4.874375 20.833271 -16.487274
4 4.704063 9.885700 5.633930
.. ... ... ...
93 3.010625 -3.796242 -3.248363
94 4.212500 -2.340933 -0.460370
95 5.563750 -0.313696 -3.006372
96 3.100312 9.047621 3.032789
97 5.100937 18.881525 12.401503
Emotion_Cingulo-Oper_L Emotion_Cingulo-Oper_R ... \
0 -0.777985 -0.353353 ...
1 -9.521039 -5.284645 ...
2 9.546204 11.319655 ...
3 1.886792 -0.946059 ...
4 9.734162 9.824339 ...
.. ... ... ...
93 -12.931731 -7.968932 ...
94 -6.904875 -13.213405 ...
95 7.014663 -1.106524 ...
96 -4.672088 -2.014852 ...
97 7.964594 -0.326323 ...
Gambling_Posterior-Mu_L Gambling_Posterior-Mu_R Gambling_Somatomotor_L \
0 -7.973004 2.530932 -3.179724
1 -24.315753 -18.506888 -6.057032
2 -1.944254 -0.950986 0.150241
3 -3.673315 -2.800902 12.236763
4 9.498112 7.589702 4.858379
.. ... ... ...
93 -4.010796 1.193511 0.801685
94 11.388163 11.611773 -12.670486
95 -1.079248 10.458447 -10.125810
96 4.350870 2.288127 -0.454990
97 -15.698724 -16.134373 -19.458602
Gambling_Somatomotor_R Gambling_Ventral-Mult_L Gambling_Ventral-Mult_R \
0 -1.810594 -7.124124 1.524933
1 4.568156 -48.646206 -11.067792
2 3.160913 -8.325856 -9.110250
3 6.242775 -9.369718 -12.720637
4 14.831399 21.459354 -7.949689
.. ... ... ...
93 -0.544744 -0.791156 22.397713
94 4.437090 1.793672 -0.470018
95 -8.503565 6.909634 26.248419
96 7.512785 10.580950 7.709618
97 -16.554394 -16.920817 -41.737430
Gambling_Visual1_L Gambling_Visual1_R Gambling_Visual2_L \
0 -3.339643 -3.025932 8.826484
1 -16.796800 -5.983401 -8.297101
2 -7.625908 -1.689586 -1.384789
3 8.636415 20.621203 9.931208
4 18.820264 10.545901 12.616854
.. ... ... ...
93 -2.309791 9.854299 -1.874123
94 -8.310730 9.031029 -6.830466
95 15.927485 13.441762 6.393254
96 0.995246 0.200687 3.556047
97 14.800047 19.709679 -5.829851
Gambling_Visual2_L.1
0 7.199637
1 6.657371
2 1.175621
3 8.350895
4 12.111169
.. ...
93 0.729667
94 -0.281131
95 4.603233
96 14.316392
97 -10.290764
[98 rows x 78 columns]
[[ 6.99446367 6.238 4.79 ... -3.0259323 8.82648362
7.19963736]
[ 7.11944444 6.70866667 10.59333333 ... -5.98340103 -8.29710147
6.65737091]
[ 9.1550865 8.34533333 11.93 ... -1.68958553 -1.38478885
1.17562126]
...
[ 11.04055556 9.28133333 10.12666667 ... 13.44176231 6.39325368
4.60323275]
[ 8.06166667 8.048 9.09 ... 0.20068705 3.5560471
14.31639195]
[ 8.51605536 7.414 7.97 ... 19.7096792 -5.82985081
-10.29076429]]
##Shuffle the data
import random
X_BOLD_rel_net_random = X_BOLD_rel_networks.copy()
# print(X_BOLD_random)
np.random.shuffle(X_BOLD_rel_net_random)
# print("\n after shuffling: ",X_BOLD_random)
#check shuffle row properly?
for i, elem in enumerate(X_BOLD_rel_net_random):
if (elem == X_BOLD_rel_networks[0]).all():
print(elem,"index: ",i)
X_IES_random = X_IES.copy()
# print("\n",X_IES_random)
np.random.shuffle(X_IES_random)
# print("\n after shuffling: ",X_IES_random)
#check shuffle row properly?
for i, elem in enumerate(X_IES_random):
if (elem == X_IES[0]).all():
print(elem,"index: ",i)
after shuffling: [[ 16.45218713 11.38416407 -3.60465966 ... 15.48796208 7.96992576
-2.74994526]
[ -0.34926509 -6.22595071 -11.57751518 ... 7.69581071 -8.43524908
7.1706866 ]
[ 14.92651966 -3.73512732 7.23280184 ... -9.79579736 7.20520023
4.20299898]
...
[ 14.4729777 -0.07256222 10.83421641 ... -2.13700959 2.33014651
9.49200178]
[-14.01305881 -11.66171774 -14.09056564 ... -0.79217031 15.67001269
14.88915906]
[ -9.10286363 3.51498535 -16.55086295 ... -11.4951203 -13.24858253
2.69033476]]
[28.43122907 0.45423503 5.57731995 -2.29266949 7.9475113 9.69271182
7.25616452 7.64897799 2.10377849 -4.40961087 0.20183027 -2.72906399
-3.17972421 -1.81059444] index: 94
[6.99446367 6.238 4.79 5.75 3.6090625 ] index: 63
# IES + shuffled bold
# merge these together
df_X_BOLD_rel_networks = data_BOLD.loc[:, list_rel_networks]
df_X_BOLD_rel_networks_shuffled = df_X_BOLD_rel_networks.sample(frac=1, random_state=42)
# NOTE we are mixing the columns of different subjects!! so one subject has features from other subjects
df_all_shuf = pd.concat([data_IES, df_X_BOLD_rel_networks_shuffled.iloc[:, 1:]], axis=1)
X_IES_BOLD_shuf = df_all_shuf.iloc[:, 1:].values
X_IES_BOLD_shuf
array([[ 6.99446367, 6.238 , 4.79 , ..., -2.72906399,
-3.17972421, -1.81059444],
[ 7.11944444, 6.70866667, 10.59333333, ..., 1.55804715,
-6.05703247, 4.56815643],
[ 9.1550865 , 8.34533333, 11.93 , ..., 7.90590405,
0.1502409 , 3.16091272],
...,
[ 11.04055556, 9.28133333, 10.12666667, ..., -16.94888299,
-10.12580988, -8.50356458],
[ 8.06166667, 8.048 , 9.09 , ..., 11.16623543,
-0.45498965, 7.51278519],
[ 8.51605536, 7.414 , 7.97 , ..., -13.64763183,
-19.45860156, -16.55439367]])
df_all = pd.concat([data_IES, data_BOLD_rel_networks.iloc[:, 1:]], axis=1)
df_all = df_all.sample(frac=1, random_state=42)
df_all
| SUBJECTS | EMOTION T1 IES | EMOTION T2 IES | SOCIAL T1 IES | SOCIAL T2 IES | GAMBLING IES | Emotion_Orbito-Affec_R | Emotion_Posterior-Mu_L | Emotion_Posterior-Mu_R | Social_Default_L | Social_Default_R | Social_Dorsal-atten_L | Social_Dorsal-atten_R | Social_Cingulo-Oper_L | Social_Cingulo-Oper_R | Gambling_Cingulo-Oper_L | Gambling_Cingulo-Oper_R | Gambling_Somatomotor_L | Gambling_Somatomotor_R | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 62 | 156233 | 9.175556 | 8.728000 | 11.347500 | 8.370 | 4.710312 | 47.444448 | -10.106824 | 16.675076 | 56.434866 | 28.182136 | 31.546946 | 42.600209 | 55.595711 | 25.529516 | -11.152869 | 2.489001 | -40.084649 | 45.352231 |
| 40 | 133928 | 8.386111 | 8.172667 | 9.883333 | 4.585 | 6.611250 | -2.774743 | -4.332258 | -4.875565 | 6.707974 | 21.594923 | 4.315081 | 5.944338 | 2.674365 | -0.610924 | 11.541634 | -8.039645 | 2.023116 | -7.822105 |
| 94 | 200614 | 7.932778 | 8.359333 | 6.043333 | 8.830 | 4.212500 | -2.153168 | -0.915092 | -11.025394 | 6.462592 | 20.029918 | 12.159982 | 28.898447 | 0.610042 | 2.912552 | -3.312991 | 5.908460 | -12.670486 | 4.437090 |
| 18 | 114924 | 7.387222 | 7.872000 | 10.575000 | 6.955 | 3.945312 | 1.288621 | 18.902996 | 19.232304 | 9.561598 | 22.492452 | -17.725834 | 9.353869 | 36.199382 | 22.825000 | -1.481654 | 11.656833 | -7.408190 | 1.623945 |
| 81 | 185139 | 7.582422 | 7.282000 | 8.196667 | 9.025 | 4.887187 | -2.815439 | 17.874201 | 5.387013 | 44.268219 | 46.451894 | 27.331754 | 29.353116 | 25.461625 | 17.506039 | 20.236217 | 12.966751 | 7.593207 | 6.259435 |
| ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... | ... |
| 60 | 153429 | 6.306111 | 6.891333 | 9.263333 | 6.960 | 4.628438 | -9.412777 | -16.422605 | -11.352146 | 33.459260 | 34.156747 | 22.302166 | 6.948978 | 19.700245 | 20.156487 | -2.216582 | 3.437919 | -1.432907 | 1.421361 |
| 71 | 162329 | 9.322222 | 9.086667 | 7.596667 | 5.810 | 4.412500 | -10.584116 | 1.107784 | 0.419456 | 16.108770 | 12.717068 | 0.852195 | 3.726035 | 3.553585 | -8.032073 | -11.537315 | -9.315438 | -2.816885 | -2.717131 |
| 14 | 111514 | 7.382222 | 7.731333 | 7.766667 | 8.095 | 2.980625 | -8.531749 | 13.911354 | 8.411415 | 13.149241 | 16.950228 | 12.188672 | 12.345472 | 3.525659 | 7.314959 | -1.239870 | -1.260985 | -5.801990 | -1.970751 |
| 92 | 199150 | 8.061667 | 7.386000 | 5.053333 | 5.330 | 3.450625 | -4.016565 | 5.786369 | 12.045751 | 57.057203 | 81.129574 | 49.524420 | 61.291128 | 54.722875 | 69.305258 | 3.976578 | -0.860398 | 0.308576 | 4.036385 |
| 51 | 148032 | 7.855225 | 6.632667 | 7.443333 | 10.120 | 3.683750 | 2.668375 | 22.794715 | 12.120931 | 9.295083 | 46.248595 | 5.619867 | 36.289513 | -5.692058 | 17.192820 | -4.886173 | -4.202818 | -8.246974 | -13.320883 |
98 rows × 19 columns
Cross Validation#
# K-Fold Cross-Validation
from sklearn.model_selection import cross_validate
def cross_validation(model, _X, _y, _cv=10):
'''Function to perform 10 Folds Cross-Validation
Parameters
----------
model: Python Class, default=None
This is the machine learning algorithm to be used for training.
_X: array
This is the matrix of features.
_y: array
This is the target variable.
_cv: int, default=10
Determines the number of folds for cross-validation.
Returns
-------
The function returns a dictionary containing the metrics 'accuracy', 'precision',
'recall', 'f1' for both training set and validation set.
'''
_scoring = ['accuracy', 'precision', 'recall', 'f1']
results = cross_validate(estimator=model,
X=_X,
y=_y,
cv=_cv,
scoring=_scoring,
return_train_score=True)
# print(len(results))
# print(results)
return {"Training Accuracy scores": results['train_accuracy'],
"Mean Training Accuracy": results['train_accuracy'].mean()*100,
"Training Precision scores": results['train_precision'],
"Mean Training Precision": results['train_precision'].mean(),
"Training Recall scores": results['train_recall'],
"Mean Training Recall": results['train_recall'].mean(),
"Training F1 scores": results['train_f1'],
"Mean Training F1 Score": results['train_f1'].mean(),
"Validation Accuracy scores": results['test_accuracy'],
"Mean Validation Accuracy": results['test_accuracy'].mean()*100,
"Validation Precision scores": results['test_precision'],
"Mean Validation Precision": results['test_precision'].mean(),
"Validation Recall scores": results['test_recall'],
"Mean Validation Recall": results['test_recall'].mean(),
"Validation F1 scores": results['test_f1'],
"Mean Validation F1 Score": results['test_f1'].mean()
}
# Grouped Bar Chart for both training and validation data
def plot_result(x_label, y_label, plot_title, train_data, val_data, num_folds=10):
'''Function to plot a grouped bar chart showing the training and validation
results of the ML model in each fold after applying K-fold cross-validation.
Parameters
----------
x_label: str,
Name of the algorithm used for training e.g 'Decision Tree'
y_label: str,
Name of metric being visualized e.g 'Accuracy'
plot_title: str,
This is the title of the plot e.g 'Accuracy Plot'
train_result: list, array
This is the list containing either training precision, accuracy, or f1 score.
val_result: list, array
This is the list containing either validation precision, accuracy, or f1 score.
Returns
-------
The function returns a Grouped Barchart showing the training and validation result
in each fold.
'''
# Set size of plot
plt.figure(figsize=(12,6))
labels = ["1st Fold", "2nd Fold", "3rd Fold", "4th Fold", "5th Fold","6th Fold", "7th Fold","8th Fold", "9th Fold","10th Fold"][:num_folds]
X_axis = np.arange(len(labels))
ax = plt.gca()
plt.ylim(0.40000, 1)
plt.bar(X_axis-0.2, train_data, 0.4, color='blue', label='Training')
plt.bar(X_axis+0.2, val_data, 0.4, color='red', label='Validation')
plt.title(plot_title, fontsize=30)
plt.xticks(X_axis, labels)
plt.xlabel(x_label, fontsize=14)
plt.ylabel(y_label, fontsize=14)
plt.legend()
plt.grid(True)
plt.show()
num_folds = 10
SVM#
1.1 IES -> personality#
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
#define the model
svm = LinearSVC(max_iter=100000)
#perform cross validation with model
#y_A
svm_result = cross_validation(svm, X_IES, y_A, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.6056099456099455
Mean Validation Accuracy 57.333333333333336
{'Training Accuracy scores': array([0.63636364, 0.67045455, 0.70454545, 0.64772727, 0.65909091,
0.69318182, 0.67045455, 0.67045455, 0.59550562, 0.65168539]),
'Mean Training Accuracy': 65.99463738508683,
'Training Precision scores': array([0.63265306, 0.66 , 0.70212766, 0.65217391, 0.66666667,
0.6875 , 0.66666667, 0.68181818, 0.59574468, 0.64583333]),
'Mean Training Precision': 0.6591184163178349,
'Training Recall scores': array([0.68888889, 0.73333333, 0.73333333, 0.66666667, 0.66666667,
0.73333333, 0.71111111, 0.66666667, 0.62222222, 0.68888889]),
'Mean Training Recall': 0.691111111111111,
'Training F1 scores': array([0.65957447, 0.69473684, 0.7173913 , 0.65934066, 0.66666667,
0.70967742, 0.68817204, 0.6741573 , 0.60869565, 0.66666667]),
'Mean Training F1 Score': 0.6745079025122479,
'Validation Accuracy scores': array([0.6 , 0.5 , 0.3 , 0.5 , 0.7 ,
0.6 , 0.6 , 0.6 , 0.77777778, 0.55555556]),
'Mean Validation Accuracy': 57.333333333333336,
'Validation Precision scores': array([0.6 , 0.5 , 0.33333333, 0.5 , 0.625 ,
0.6 , 0.57142857, 0.57142857, 0.8 , 0.6 ]),
'Mean Validation Precision': 0.5701190476190476,
'Validation Recall scores': array([0.6, 0.4, 0.4, 0.6, 1. , 0.6, 0.8, 0.8, 0.8, 0.6]),
'Mean Validation Recall': 0.6599999999999999,
'Validation F1 scores': array([0.6 , 0.44444444, 0.36363636, 0.54545455, 0.76923077,
0.6 , 0.66666667, 0.66666667, 0.8 , 0.6 ]),
'Mean Validation F1 Score': 0.6056099456099455}
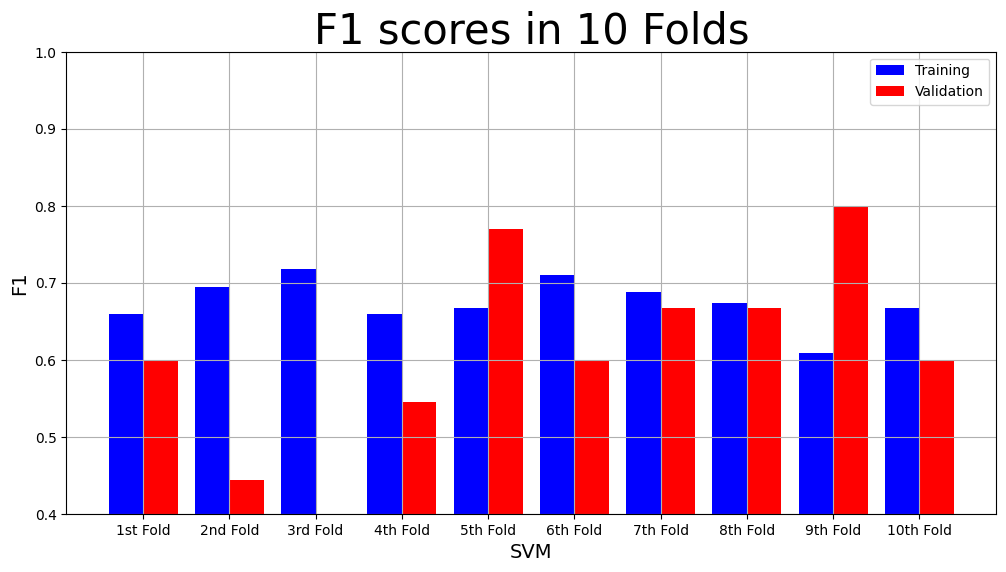
model_name = "SVM"
plot_result(model_name,
"F1",
"F1 scores in 10 Folds",
svm_result["Training F1 scores"],
svm_result["Validation F1 scores"])
#y_O
#define the model
svm = LinearSVC(max_iter=100000)
svm_result = cross_validation(svm, X_IES, y_O, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.5646176046176047
Mean Validation Accuracy 53.333333333333336
{'Training Accuracy scores': array([0.57954545, 0.61363636, 0.54545455, 0.63636364, 0.60227273,
0.57954545, 0.59090909, 0.51136364, 0.5505618 , 0.53932584]),
'Mean Training Accuracy': 57.48978549540347,
'Training Precision scores': array([0.58333333, 0.60377358, 0.54901961, 0.62264151, 0.61904762,
0.58695652, 0.60465116, 0.52 , 0.55319149, 0.54 ]),
'Mean Training Precision': 0.5782614828455243,
'Training Recall scores': array([0.62222222, 0.71111111, 0.62222222, 0.73333333, 0.57777778,
0.6 , 0.57777778, 0.57777778, 0.57777778, 0.6 ]),
'Mean Training Recall': 0.6199999999999999,
'Training F1 scores': array([0.60215054, 0.65306122, 0.58333333, 0.67346939, 0.59770115,
0.59340659, 0.59090909, 0.54736842, 0.56521739, 0.56842105]),
'Mean Training F1 Score': 0.5975038181942168,
'Validation Accuracy scores': array([0.4 , 0.6 , 0.8 , 0.5 , 0.3 ,
0.4 , 0.4 , 0.6 , 0.77777778, 0.55555556]),
'Mean Validation Accuracy': 53.333333333333336,
'Validation Precision scores': array([0.44444444, 0.66666667, 0.8 , 0.5 , 0.33333333,
0.42857143, 0.4 , 0.6 , 0.8 , 0.57142857]),
'Mean Validation Precision': 0.5544444444444444,
'Validation Recall scores': array([0.8, 0.4, 0.8, 0.4, 0.4, 0.6, 0.4, 0.6, 0.8, 0.8]),
'Mean Validation Recall': 0.6,
'Validation F1 scores': array([0.57142857, 0.5 , 0.8 , 0.44444444, 0.36363636,
0.5 , 0.4 , 0.6 , 0.8 , 0.66666667]),
'Mean Validation F1 Score': 0.5646176046176047}
#y_C
#define the model
svm = LinearSVC(max_iter=100000)
svm_result = cross_validation(svm, X_IES, y_C, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.5350305250305251
Mean Validation Accuracy 42.77777777777778
{'Training Accuracy scores': array([0.56818182, 0.55681818, 0.60227273, 0.52272727, 0.55681818,
0.52272727, 0.57954545, 0.59090909, 0.57303371, 0.61797753]),
'Mean Training Accuracy': 56.91011235955056,
'Training Precision scores': array([0.56666667, 0.56603774, 0.59677419, 0.53731343, 0.56451613,
0.54385965, 0.59615385, 0.59322034, 0.57377049, 0.61403509]),
'Mean Training Precision': 0.575234757171447,
'Training Recall scores': array([0.73913043, 0.65217391, 0.78723404, 0.76595745, 0.74468085,
0.65957447, 0.65957447, 0.74468085, 0.74468085, 0.74468085]),
'Mean Training Recall': 0.7242368177613321,
'Training F1 scores': array([0.64150943, 0.60606061, 0.67889908, 0.63157895, 0.64220183,
0.59615385, 0.62626263, 0.66037736, 0.64814815, 0.67307692]),
'Mean Training F1 Score': 0.6404268806954594,
'Validation Accuracy scores': array([0.6 , 0.2 , 0.4 , 0.6 , 0.4 ,
0.5 , 0.4 , 0.4 , 0.44444444, 0.33333333]),
'Mean Validation Accuracy': 42.77777777777778,
'Validation Precision scores': array([0.75 , 0.33333333, 0.42857143, 0.55555556, 0.44444444,
0.5 , 0.42857143, 0.44444444, 0.5 , 0.42857143]),
'Mean Validation Precision': 0.4813492063492063,
'Validation Recall scores': array([0.5 , 0.33333333, 0.6 , 1. , 0.8 ,
0.8 , 0.6 , 0.8 , 0.4 , 0.6 ]),
'Mean Validation Recall': 0.6433333333333333,
'Validation F1 scores': array([0.6 , 0.33333333, 0.5 , 0.71428571, 0.57142857,
0.61538462, 0.5 , 0.57142857, 0.44444444, 0.5 ]),
'Mean Validation F1 Score': 0.5350305250305251}
y_N
#define the model
svm = LinearSVC(max_iter=100000)
svm_result = cross_validation(svm, X_IES, y_N, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.514032634032634
Mean Validation Accuracy 49.222222222222214
{'Training Accuracy scores': array([0.61363636, 0.61363636, 0.60227273, 0.61363636, 0.56818182,
0.61363636, 0.625 , 0.61363636, 0.62921348, 0.57303371]),
'Mean Training Accuracy': 60.658835546476,
'Training Precision scores': array([0.63265306, 0.62745098, 0.62 , 0.63265306, 0.59574468,
0.63829787, 0.63829787, 0.63043478, 0.64583333, 0.58823529]),
'Mean Training Precision': 0.6249600938432727,
'Training Recall scores': array([0.65957447, 0.68085106, 0.65957447, 0.65957447, 0.59574468,
0.63829787, 0.65217391, 0.63043478, 0.65957447, 0.63829787]),
'Mean Training Recall': 0.64740980573543,
'Training F1 scores': array([0.64583333, 0.65306122, 0.63917526, 0.64583333, 0.59574468,
0.63829787, 0.64516129, 0.63043478, 0.65263158, 0.6122449 ]),
'Mean Training F1 Score': 0.6358418251917739,
'Validation Accuracy scores': array([0.5 , 0.4 , 0.3 , 0.6 , 0.6 ,
0.3 , 0.6 , 0.4 , 0.44444444, 0.77777778]),
'Mean Validation Accuracy': 49.222222222222214,
'Validation Precision scores': array([0.5 , 0.42857143, 0.25 , 0.57142857, 0.66666667,
0.375 , 1. , 0.5 , 0.5 , 0.8 ]),
'Mean Validation Precision': 0.5591666666666666,
'Validation Recall scores': array([0.6 , 0.6 , 0.2 , 0.8 , 0.4 ,
0.6 , 0.33333333, 0.5 , 0.4 , 0.8 ]),
'Mean Validation Recall': 0.5233333333333333,
'Validation F1 scores': array([0.54545455, 0.5 , 0.22222222, 0.66666667, 0.5 ,
0.46153846, 0.5 , 0.5 , 0.44444444, 0.8 ]),
'Mean Validation F1 Score': 0.514032634032634}
#y_E
#define the model
svm = LinearSVC(max_iter=100000)
svm_result = cross_validation(svm, X_IES, y_E, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.631042291042291
Mean Validation Accuracy 58.33333333333333
{'Training Accuracy scores': array([0.61363636, 0.60227273, 0.625 , 0.63636364, 0.64772727,
0.59090909, 0.56818182, 0.61363636, 0.60674157, 0.61797753]),
'Mean Training Accuracy': 61.22446373850868,
'Training Precision scores': array([0.6 , 0.59016393, 0.61016949, 0.61290323, 0.63157895,
0.58928571, 0.5625 , 0.60714286, 0.59649123, 0.60714286]),
'Mean Training Precision': 0.600737825576813,
'Training Recall scores': array([0.73333333, 0.7826087 , 0.7826087 , 0.82608696, 0.7826087 ,
0.7173913 , 0.7826087 , 0.73913043, 0.73913043, 0.73913043]),
'Mean Training Recall': 0.7624637681159421,
'Training F1 scores': array([0.66 , 0.6728972 , 0.68571429, 0.7037037 , 0.69902913,
0.64705882, 0.65454545, 0.66666667, 0.66019417, 0.66666667]),
'Mean Training F1 Score': 0.6716476098058746,
'Validation Accuracy scores': array([0.6 , 0.7 , 0.3 , 0.4 , 0.5 ,
0.7 , 0.7 , 0.6 , 0.77777778, 0.55555556]),
'Mean Validation Accuracy': 58.33333333333333,
'Validation Precision scores': array([0.75 , 0.66666667, 0.375 , 0.4 , 0.5 ,
1. , 0.625 , 0.55555556, 0.8 , 0.6 ]),
'Mean Validation Precision': 0.6272222222222221,
'Validation Recall scores': array([0.5, 0.8, 0.6, 0.4, 1. , 0.4, 1. , 1. , 0.8, 0.6]),
'Mean Validation Recall': 0.7099999999999999,
'Validation F1 scores': array([0.6 , 0.72727273, 0.46153846, 0.4 , 0.66666667,
0.57142857, 0.76923077, 0.71428571, 0.8 , 0.6 ]),
'Mean Validation F1 Score': 0.631042291042291}
1.2 IES + relevant BOLD -> personality#
#y_A Try bold only
#define the model
svm = LinearSVC(max_iter=10000)
#perform cross validation with model
svm_result = cross_validation(svm, X_BOLD_rel_networks, y_A, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
The main results are
Mean Validation F1: 0.538811188811189
Mean Validation Accuracy 54.22222222222223
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
{'Training Accuracy scores': array([0.61363636, 0.72727273, 0.63636364, 0.65909091, 0.70454545,
0.64772727, 0.67045455, 0.69318182, 0.62921348, 0.59550562]),
'Mean Training Accuracy': 65.76991828396321,
'Training Precision scores': array([0.63414634, 0.68421053, 0.76 , 0.68292683, 0.69387755,
0.625 , 0.68181818, 0.66666667, 0.61538462, 0.59183673]),
'Mean Training Precision': 0.6635867446631247,
'Training Recall scores': array([0.57777778, 0.86666667, 0.42222222, 0.62222222, 0.75555556,
0.77777778, 0.66666667, 0.8 , 0.71111111, 0.64444444]),
'Mean Training Recall': 0.6844444444444445,
'Training F1 scores': array([0.60465116, 0.76470588, 0.54285714, 0.65116279, 0.72340426,
0.69306931, 0.6741573 , 0.72727273, 0.65979381, 0.61702128]),
'Mean Training F1 Score': 0.6658095662620547,
'Validation Accuracy scores': array([0.8 , 0.4 , 0.6 , 0.5 , 0.6 ,
0.4 , 0.4 , 0.5 , 0.66666667, 0.55555556]),
'Mean Validation Accuracy': 54.22222222222223,
'Validation Precision scores': array([1. , 0.33333333, 0.66666667, 0.5 , 0.6 ,
0.42857143, 0.4 , 0.5 , 0.66666667, 0.66666667]),
'Mean Validation Precision': 0.5761904761904763,
'Validation Recall scores': array([0.6, 0.2, 0.4, 0.6, 0.6, 0.6, 0.4, 0.8, 0.8, 0.4]),
'Mean Validation Recall': 0.54,
'Validation F1 scores': array([0.75 , 0.25 , 0.5 , 0.54545455, 0.6 ,
0.5 , 0.4 , 0.61538462, 0.72727273, 0.5 ]),
'Mean Validation F1 Score': 0.538811188811189}
#y_A combined
#define the model
svm = LinearSVC(max_iter=1000000)
#perform cross validation with model
svm_result = cross_validation(svm, X_combined, y_A, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.566868686868687
Mean Validation Accuracy 55.33333333333334
{'Training Accuracy scores': array([0.75 , 0.77272727, 0.75 , 0.84090909, 0.72727273,
0.69318182, 0.73863636, 0.76136364, 0.73033708, 0.7752809 ]),
'Mean Training Accuracy': 75.39708886618999,
'Training Precision scores': array([0.74468085, 0.77777778, 0.75555556, 0.87804878, 0.75609756,
0.71428571, 0.775 , 0.77272727, 0.73333333, 0.79069767]),
'Mean Training Precision': 0.7698204520625502,
'Training Recall scores': array([0.77777778, 0.77777778, 0.75555556, 0.8 , 0.68888889,
0.66666667, 0.68888889, 0.75555556, 0.73333333, 0.75555556]),
'Mean Training Recall': 0.74,
'Training F1 scores': array([0.76086957, 0.77777778, 0.75555556, 0.8372093 , 0.72093023,
0.68965517, 0.72941176, 0.76404494, 0.73333333, 0.77272727]),
'Mean Training F1 Score': 0.7541514920434951,
'Validation Accuracy scores': array([0.9 , 0.3 , 0.5 , 0.5 , 0.7 ,
0.4 , 0.4 , 0.5 , 0.66666667, 0.66666667]),
'Mean Validation Accuracy': 55.33333333333334,
'Validation Precision scores': array([1. , 0.25 , 0.5 , 0.5 , 0.66666667,
0.4 , 0.4 , 0.5 , 0.66666667, 0.75 ]),
'Mean Validation Precision': 0.5633333333333334,
'Validation Recall scores': array([0.8, 0.2, 0.6, 0.6, 0.8, 0.4, 0.4, 0.6, 0.8, 0.6]),
'Mean Validation Recall': 0.58,
'Validation F1 scores': array([0.88888889, 0.22222222, 0.54545455, 0.54545455, 0.72727273,
0.4 , 0.4 , 0.54545455, 0.72727273, 0.66666667]),
'Mean Validation F1 Score': 0.566868686868687}
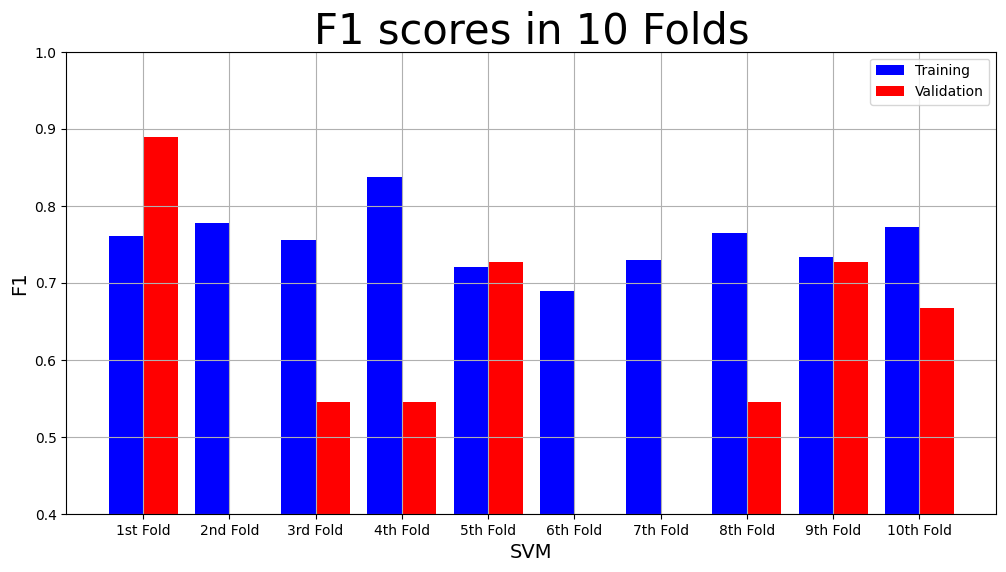
model_name = "SVM"
plot_result(model_name,
"F1",
"F1 scores in 10 Folds",
svm_result["Training F1 scores"],
svm_result["Validation F1 scores"])
#y_O combined
#define the model
svm = LinearSVC(max_iter=1000000)
#perform cross validation with model
svm_result = cross_validation(svm, X_combined, y_O, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.45732323232323235
Mean Validation Accuracy 49.11111111111111
{'Training Accuracy scores': array([0.67045455, 0.70454545, 0.68181818, 0.67045455, 0.69318182,
0.72727273, 0.70454545, 0.63636364, 0.68539326, 0.66292135]),
'Mean Training Accuracy': 68.36950970377936,
'Training Precision scores': array([0.66 , 0.73170732, 0.68888889, 0.68181818, 0.71428571,
0.73333333, 0.74358974, 0.63265306, 0.72972973, 0.6744186 ]),
'Mean Training Precision': 0.6990424574594416,
'Training Recall scores': array([0.73333333, 0.66666667, 0.68888889, 0.66666667, 0.66666667,
0.73333333, 0.64444444, 0.68888889, 0.6 , 0.64444444]),
'Mean Training Recall': 0.6733333333333333,
'Training F1 scores': array([0.69473684, 0.69767442, 0.68888889, 0.6741573 , 0.68965517,
0.73333333, 0.69047619, 0.65957447, 0.65853659, 0.65909091]),
'Mean Training F1 Score': 0.6846124111734776,
'Validation Accuracy scores': array([0.6 , 0.6 , 0.2 , 0.5 , 0.2 ,
0.5 , 0.4 , 0.8 , 0.55555556, 0.55555556]),
'Mean Validation Accuracy': 49.11111111111111,
'Validation Precision scores': array([0.57142857, 0.57142857, 0. , 0.5 , 0. ,
0.5 , 0.33333333, 0.8 , 0.6 , 0.6 ]),
'Mean Validation Precision': 0.44761904761904764,
'Validation Recall scores': array([0.8, 0.8, 0. , 0.6, 0. , 0.4, 0.2, 0.8, 0.6, 0.6]),
'Mean Validation Recall': 0.48,
'Validation F1 scores': array([0.66666667, 0.66666667, 0. , 0.54545455, 0. ,
0.44444444, 0.25 , 0.8 , 0.6 , 0.6 ]),
'Mean Validation F1 Score': 0.45732323232323235}
#y_C combined
#define the model
svm = LinearSVC(max_iter=1000000)
#perform cross validation with model
svm_result = cross_validation(svm, X_combined, y_C, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.5745687645687647
Mean Validation Accuracy 51.888888888888886
{'Training Accuracy scores': array([0.68181818, 0.69318182, 0.70454545, 0.70454545, 0.68181818,
0.65909091, 0.63636364, 0.71590909, 0.71910112, 0.74157303]),
'Mean Training Accuracy': 69.37946884576098,
'Training Precision scores': array([0.6875 , 0.71111111, 0.71428571, 0.71428571, 0.69387755,
0.68085106, 0.64705882, 0.69642857, 0.72916667, 0.75 ]),
'Mean Training Precision': 0.7024565216157386,
'Training Recall scores': array([0.7173913 , 0.69565217, 0.74468085, 0.74468085, 0.72340426,
0.68085106, 0.70212766, 0.82978723, 0.74468085, 0.76595745]),
'Mean Training Recall': 0.7349213691026827,
'Training F1 scores': array([0.70212766, 0.7032967 , 0.72916667, 0.72916667, 0.70833333,
0.68085106, 0.67346939, 0.75728155, 0.73684211, 0.75789474]),
'Mean Training F1 Score': 0.7178429876626047,
'Validation Accuracy scores': array([0.9 , 0.3 , 0.5 , 0.8 , 0.4 ,
0.5 , 0.4 , 0.5 , 0.55555556, 0.33333333]),
'Mean Validation Accuracy': 51.888888888888886,
'Validation Precision scores': array([1. , 0.4 , 0.5 , 0.8 , 0.4 ,
0.5 , 0.4 , 0.5 , 0.57142857, 0.42857143]),
'Mean Validation Precision': 0.55,
'Validation Recall scores': array([0.83333333, 0.33333333, 0.6 , 0.8 , 0.4 ,
0.8 , 0.4 , 0.6 , 0.8 , 0.6 ]),
'Mean Validation Recall': 0.6166666666666666,
'Validation F1 scores': array([0.90909091, 0.36363636, 0.54545455, 0.8 , 0.4 ,
0.61538462, 0.4 , 0.54545455, 0.66666667, 0.5 ]),
'Mean Validation F1 Score': 0.5745687645687647}
#y_N combined
#define the model
svm = LinearSVC(max_iter=1000000)
#perform cross validation with model
svm_result = cross_validation(svm, X_combined, y_N, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.5548701298701297
Mean Validation Accuracy 54.0
{'Training Accuracy scores': array([0.69318182, 0.67045455, 0.70454545, 0.76136364, 0.75 ,
0.70454545, 0.67045455, 0.73863636, 0.71910112, 0.73033708]),
'Mean Training Accuracy': 71.4262002042901,
'Training Precision scores': array([0.70833333, 0.6875 , 0.71428571, 0.76 , 0.75510204,
0.71428571, 0.68085106, 0.74468085, 0.73913043, 0.75555556]),
'Mean Training Precision': 0.725972470795287,
'Training Recall scores': array([0.72340426, 0.70212766, 0.74468085, 0.80851064, 0.78723404,
0.74468085, 0.69565217, 0.76086957, 0.72340426, 0.72340426]),
'Mean Training Recall': 0.7413968547641074,
'Training F1 scores': array([0.71578947, 0.69473684, 0.72916667, 0.78350515, 0.77083333,
0.72916667, 0.68817204, 0.75268817, 0.7311828 , 0.73913043]),
'Mean Training F1 Score': 0.7334371582630613,
'Validation Accuracy scores': array([0.4 , 0.7 , 0.5 , 0.5 , 0.5 ,
0.6 , 0.8 , 0.4 , 0.66666667, 0.33333333]),
'Mean Validation Accuracy': 54.0,
'Validation Precision scores': array([0.42857143, 0.66666667, 0.5 , 0.5 , 0.5 ,
0.57142857, 0.83333333, 0.5 , 0.75 , 0.33333333]),
'Mean Validation Precision': 0.5583333333333333,
'Validation Recall scores': array([0.6 , 0.8 , 0.4 , 0.4 , 0.4 ,
0.8 , 0.83333333, 0.66666667, 0.6 , 0.2 ]),
'Mean Validation Recall': 0.5700000000000001,
'Validation F1 scores': array([0.5 , 0.72727273, 0.44444444, 0.44444444, 0.44444444,
0.66666667, 0.83333333, 0.57142857, 0.66666667, 0.25 ]),
'Mean Validation F1 Score': 0.5548701298701297}
#y_E combined
#define the model
svm = LinearSVC(max_iter=1000000)
#perform cross validation with model
svm_result = cross_validation(svm, X_combined, y_E, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.5316300366300366
Mean Validation Accuracy 51.22222222222222
{'Training Accuracy scores': array([0.68181818, 0.68181818, 0.68181818, 0.69318182, 0.69318182,
0.69318182, 0.67045455, 0.75 , 0.68539326, 0.65168539]),
'Mean Training Accuracy': 68.82533197139938,
'Training Precision scores': array([0.68888889, 0.69565217, 0.67307692, 0.67924528, 0.69387755,
0.68627451, 0.66666667, 0.75 , 0.68 , 0.65306122]),
'Mean Training Precision': 0.6866743220878515,
'Training Recall scores': array([0.68888889, 0.69565217, 0.76086957, 0.7826087 , 0.73913043,
0.76086957, 0.73913043, 0.7826087 , 0.73913043, 0.69565217]),
'Mean Training Recall': 0.7384541062801933,
'Training F1 scores': array([0.68888889, 0.69565217, 0.71428571, 0.72727273, 0.71578947,
0.72164948, 0.70103093, 0.76595745, 0.70833333, 0.67368421]),
'Mean Training F1 Score': 0.7112544381083878,
'Validation Accuracy scores': array([0.5 , 0.6 , 0.4 , 0.3 , 0.3 ,
0.8 , 0.4 , 0.6 , 0.66666667, 0.55555556]),
'Mean Validation Accuracy': 51.22222222222222,
'Validation Precision scores': array([0.66666667, 0.6 , 0.42857143, 0.25 , 0.375 ,
1. , 0.44444444, 0.6 , 0.75 , 0.66666667]),
'Mean Validation Precision': 0.5781349206349207,
'Validation Recall scores': array([0.33333333, 0.6 , 0.6 , 0.2 , 0.6 ,
0.6 , 0.8 , 0.6 , 0.6 , 0.4 ]),
'Mean Validation Recall': 0.5333333333333333,
'Validation F1 scores': array([0.44444444, 0.6 , 0.5 , 0.22222222, 0.46153846,
0.75 , 0.57142857, 0.6 , 0.66666667, 0.5 ]),
'Mean Validation F1 Score': 0.5316300366300366}
1.3 IES + all networks -> personality#
# (X_combined_all)
#y_A combined
#define the model
svm = LinearSVC(max_iter=900000)
#perform cross validation with model
svm_result = cross_validation(svm, X_combined_all, y_A, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.4688888888888889
Mean Validation Accuracy 47.111111111111114
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.4 , 0.5 , 0.6 , 0.4 , 0.5 ,
0.4 , 0.4 , 0.4 , 0.55555556, 0.55555556]),
'Mean Validation Accuracy': 47.111111111111114,
'Validation Precision scores': array([0.4 , 0.5 , 0.6 , 0.42857143, 0.5 ,
0.4 , 0.4 , 0.4 , 0.66666667, 0.6 ]),
'Mean Validation Precision': 0.48952380952380947,
'Validation Recall scores': array([0.4, 0.4, 0.6, 0.6, 0.4, 0.4, 0.4, 0.4, 0.4, 0.6]),
'Mean Validation Recall': 0.45999999999999996,
'Validation F1 scores': array([0.4 , 0.44444444, 0.6 , 0.5 , 0.44444444,
0.4 , 0.4 , 0.4 , 0.5 , 0.6 ]),
'Mean Validation F1 Score': 0.4688888888888889}
#y_O
svm = LinearSVC(max_iter=900000)
#perform cross validation with model
svm_result = cross_validation(svm, X_combined_all, y_O, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.5775757575757575
Mean Validation Accuracy 57.111111111111114
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.7 , 0.5 , 0.6 , 0.6 , 0.3 ,
0.3 , 0.8 , 0.8 , 0.44444444, 0.66666667]),
'Mean Validation Accuracy': 57.111111111111114,
'Validation Precision scores': array([0.75 , 0.5 , 0.57142857, 0.6 , 0.25 ,
0.33333333, 0.8 , 0.8 , 0.5 , 0.75 ]),
'Mean Validation Precision': 0.5854761904761905,
'Validation Recall scores': array([0.6, 0.6, 0.8, 0.6, 0.2, 0.4, 0.8, 0.8, 0.4, 0.6]),
'Mean Validation Recall': 0.58,
'Validation F1 scores': array([0.66666667, 0.54545455, 0.66666667, 0.6 , 0.22222222,
0.36363636, 0.8 , 0.8 , 0.44444444, 0.66666667]),
'Mean Validation F1 Score': 0.5775757575757575}
#y_C
svm = LinearSVC(max_iter=900000)
#perform cross validation with model
svm_result = cross_validation(svm, X_combined_all, y_C, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.5012987012987014
Mean Validation Accuracy 52.666666666666664
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.6 , 0.6 , 0.4 , 0.4 , 0.8 ,
0.7 , 0.6 , 0.5 , 0.55555556, 0.11111111]),
'Mean Validation Accuracy': 52.666666666666664,
'Validation Precision scores': array([1. , 0.75 , 0.4 , 0.42857143, 0.71428571,
0.66666667, 0.57142857, 0.5 , 0.66666667, 0. ]),
'Mean Validation Precision': 0.5697619047619048,
'Validation Recall scores': array([0.33333333, 0.5 , 0.4 , 0.6 , 1. ,
0.8 , 0.8 , 0.2 , 0.4 , 0. ]),
'Mean Validation Recall': 0.5033333333333333,
'Validation F1 scores': array([0.5 , 0.6 , 0.4 , 0.5 , 0.83333333,
0.72727273, 0.66666667, 0.28571429, 0.5 , 0. ]),
'Mean Validation F1 Score': 0.5012987012987014}
#y_N
svm = LinearSVC(max_iter=900000)
#perform cross validation with model
svm_result = cross_validation(svm, X_combined_all, y_N, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.5911111111111111
Mean Validation Accuracy 58.22222222222222
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.9 , 0.5 , 0.8 , 0.5 , 0.6 ,
0.4 , 0.4 , 0.5 , 0.77777778, 0.44444444]),
'Mean Validation Accuracy': 58.22222222222222,
'Validation Precision scores': array([0.83333333, 0.5 , 0.8 , 0.5 , 0.6 ,
0.4 , 0.5 , 0.6 , 1. , 0.5 ]),
'Mean Validation Precision': 0.6233333333333334,
'Validation Recall scores': array([1. , 0.4 , 0.8 , 1. , 0.6 ,
0.4 , 0.16666667, 0.5 , 0.6 , 0.6 ]),
'Mean Validation Recall': 0.6066666666666667,
'Validation F1 scores': array([0.90909091, 0.44444444, 0.8 , 0.66666667, 0.6 ,
0.4 , 0.25 , 0.54545455, 0.75 , 0.54545455]),
'Mean Validation F1 Score': 0.5911111111111111}
#y_E
svm = LinearSVC(max_iter=900000)
#perform cross validation with model
svm_result = cross_validation(svm, X_combined_all, y_E, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.5813919413919414
Mean Validation Accuracy 57.44444444444443
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.6 , 0.3 , 0.6 , 0.7 , 0.7 ,
0.6 , 0.5 , 0.3 , 0.66666667, 0.77777778]),
'Mean Validation Accuracy': 57.44444444444443,
'Validation Precision scores': array([0.75 , 0.375 , 0.57142857, 0.66666667, 0.66666667,
0.55555556, 0.5 , 0. , 1. , 0.8 ]),
'Mean Validation Precision': 0.5885317460317461,
'Validation Recall scores': array([0.5, 0.6, 0.8, 0.8, 0.8, 1. , 0.6, 0. , 0.4, 0.8]),
'Mean Validation Recall': 0.63,
'Validation F1 scores': array([0.6 , 0.46153846, 0.66666667, 0.72727273, 0.72727273,
0.71428571, 0.54545455, 0. , 0.57142857, 0.8 ]),
'Mean Validation F1 Score': 0.5813919413919414}
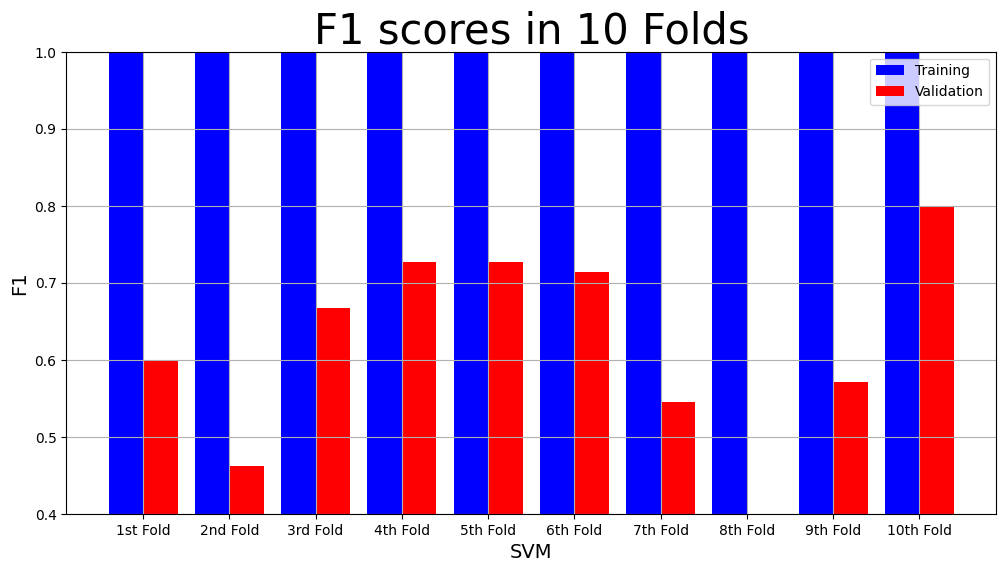
model_name = "SVM"
plot_result(model_name,
"F1",
"F1 scores in 10 Folds",
svm_result["Training F1 scores"],
svm_result["Validation F1 scores"])
2.1 shuffled IES -> personality#
#define the model #X_IES_random
svm = LinearSVC(max_iter=100000)
#perform cross validation with model
#y_A
svm_result = cross_validation(svm, X_IES_random, y_A, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.534978354978355
Mean Validation Accuracy 56.33333333333334
{'Training Accuracy scores': array([0.61363636, 0.61363636, 0.60227273, 0.61363636, 0.65909091,
0.60227273, 0.60227273, 0.59090909, 0.61797753, 0.57303371]),
'Mean Training Accuracy': 60.8873850868233,
'Training Precision scores': array([0.62790698, 0.65714286, 0.61904762, 0.63414634, 0.7027027 ,
0.61904762, 0.63157895, 0.61538462, 0.64102564, 0.58974359]),
'Mean Training Precision': 0.6337726909670667,
'Training Recall scores': array([0.6 , 0.51111111, 0.57777778, 0.57777778, 0.57777778,
0.57777778, 0.53333333, 0.53333333, 0.55555556, 0.51111111]),
'Mean Training Recall': 0.5555555555555556,
'Training F1 scores': array([0.61363636, 0.575 , 0.59770115, 0.60465116, 0.63414634,
0.59770115, 0.57831325, 0.57142857, 0.5952381 , 0.54761905]),
'Mean Training F1 Score': 0.5915435134038812,
'Validation Accuracy scores': array([0.8 , 0.5 , 0.4 , 0.4 , 0.4 ,
0.4 , 0.7 , 0.7 , 0.44444444, 0.88888889]),
'Mean Validation Accuracy': 56.33333333333334,
'Validation Precision scores': array([0.8 , 0.5 , 0.42857143, 0.44444444, 0.33333333,
0.33333333, 1. , 0.75 , 0.5 , 0.83333333]),
'Mean Validation Precision': 0.5923015873015873,
'Validation Recall scores': array([0.8, 0.6, 0.6, 0.8, 0.2, 0.2, 0.4, 0.6, 0.2, 1. ]),
'Mean Validation Recall': 0.5399999999999999,
'Validation F1 scores': array([0.8 , 0.54545455, 0.5 , 0.57142857, 0.25 ,
0.25 , 0.57142857, 0.66666667, 0.28571429, 0.90909091]),
'Mean Validation F1 Score': 0.534978354978355}
#y_O
svm = LinearSVC(max_iter=100000)
#perform cross validation with model
svm_result = cross_validation(svm, X_IES_random, y_O, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.557965367965368
Mean Validation Accuracy 59.77777777777777
{'Training Accuracy scores': array([0.63636364, 0.65909091, 0.71590909, 0.625 , 0.68181818,
0.64772727, 0.72727273, 0.70454545, 0.68539326, 0.66292135]),
'Mean Training Accuracy': 67.46041879468847,
'Training Precision scores': array([0.66666667, 0.7027027 , 0.76315789, 0.65 , 0.69767442,
0.68421053, 0.76923077, 0.74358974, 0.72972973, 0.7027027 ]),
'Mean Training Precision': 0.7109665154279597,
'Training Recall scores': array([0.57777778, 0.57777778, 0.64444444, 0.57777778, 0.66666667,
0.57777778, 0.66666667, 0.64444444, 0.6 , 0.57777778]),
'Mean Training Recall': 0.611111111111111,
'Training F1 scores': array([0.61904762, 0.63414634, 0.69879518, 0.61176471, 0.68181818,
0.62650602, 0.71428571, 0.69047619, 0.65853659, 0.63414634]),
'Mean Training F1 Score': 0.6569522884622018,
'Validation Accuracy scores': array([0.7 , 0.7 , 0.6 , 0.8 , 0.4 ,
0.8 , 0.4 , 0.8 , 0.44444444, 0.33333333]),
'Mean Validation Accuracy': 59.77777777777777,
'Validation Precision scores': array([0.75 , 0.66666667, 0.6 , 0.8 , 0.33333333,
0.8 , 0.33333333, 0.8 , 0.5 , 0.4 ]),
'Mean Validation Precision': 0.5983333333333334,
'Validation Recall scores': array([0.6, 0.8, 0.6, 0.8, 0.2, 0.8, 0.2, 0.8, 0.2, 0.4]),
'Mean Validation Recall': 0.54,
'Validation F1 scores': array([0.66666667, 0.72727273, 0.6 , 0.8 , 0.25 ,
0.8 , 0.25 , 0.8 , 0.28571429, 0.4 ]),
'Mean Validation F1 Score': 0.557965367965368}
#y_C
svm = LinearSVC(max_iter=100000)
#perform cross validation with model
svm_result = cross_validation(svm, X_IES_random, y_C, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.5677489177489178
Mean Validation Accuracy 50.777777777777786
{'Training Accuracy scores': array([0.61363636, 0.625 , 0.61363636, 0.59090909, 0.625 ,
0.625 , 0.59090909, 0.57954545, 0.66292135, 0.65168539]),
'Mean Training Accuracy': 61.78243105209397,
'Training Precision scores': array([0.61538462, 0.62264151, 0.61016949, 0.59322034, 0.625 ,
0.625 , 0.59322034, 0.59615385, 0.64912281, 0.63793103]),
'Mean Training Precision': 0.6167843981964252,
'Training Recall scores': array([0.69565217, 0.7173913 , 0.76595745, 0.74468085, 0.74468085,
0.74468085, 0.74468085, 0.65957447, 0.78723404, 0.78723404]),
'Mean Training Recall': 0.7391766882516189,
'Training F1 scores': array([0.65306122, 0.66666667, 0.67924528, 0.66037736, 0.67961165,
0.67961165, 0.66037736, 0.62626263, 0.71153846, 0.7047619 ]),
'Mean Training F1 Score': 0.6721514184690329,
'Validation Accuracy scores': array([0.6 , 0.4 , 0.7 , 0.4 , 0.6 ,
0.5 , 0.5 , 0.6 , 0.22222222, 0.55555556]),
'Mean Validation Accuracy': 50.777777777777786,
'Validation Precision scores': array([0.66666667, 0.5 , 0.66666667, 0.44444444, 0.57142857,
0.5 , 0.5 , 0.57142857, 0.25 , 0.57142857]),
'Mean Validation Precision': 0.5242063492063492,
'Validation Recall scores': array([0.66666667, 0.5 , 0.8 , 0.8 , 0.8 ,
0.6 , 0.4 , 0.8 , 0.2 , 0.8 ]),
'Mean Validation Recall': 0.6366666666666667,
'Validation F1 scores': array([0.66666667, 0.5 , 0.72727273, 0.57142857, 0.66666667,
0.54545455, 0.44444444, 0.66666667, 0.22222222, 0.66666667]),
'Mean Validation F1 Score': 0.5677489177489178}
#y_N
svm = LinearSVC(max_iter=90000)
#perform cross validation with model
svm_result = cross_validation(svm, X_IES_random, y_N, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.5483605283605283
Mean Validation Accuracy 50.22222222222222
{'Training Accuracy scores': array([0.61363636, 0.57954545, 0.60227273, 0.53409091, 0.59090909,
0.56818182, 0.51136364, 0.55681818, 0.58426966, 0.56179775]),
'Mean Training Accuracy': 57.02885597548518,
'Training Precision scores': array([0.63265306, 0.58928571, 0.60344828, 0.55172414, 0.59322034,
0.58181818, 0.52727273, 0.56140351, 0.59259259, 0.57142857]),
'Mean Training Precision': 0.5804847110170361,
'Training Recall scores': array([0.65957447, 0.70212766, 0.74468085, 0.68085106, 0.74468085,
0.68085106, 0.63043478, 0.69565217, 0.68085106, 0.68085106]),
'Mean Training Recall': 0.6900555041628122,
'Training F1 scores': array([0.64583333, 0.6407767 , 0.66666667, 0.60952381, 0.66037736,
0.62745098, 0.57425743, 0.62135922, 0.63366337, 0.62135922]),
'Mean Training F1 Score': 0.6301268086116807,
'Validation Accuracy scores': array([0.4 , 0.4 , 0.2 , 0.7 , 0.4 ,
0.7 , 0.5 , 0.5 , 0.55555556, 0.66666667]),
'Mean Validation Accuracy': 50.22222222222222,
'Validation Precision scores': array([0.42857143, 0.42857143, 0.2 , 0.66666667, 0.4 ,
0.625 , 0.66666667, 0.57142857, 0.6 , 0.66666667]),
'Mean Validation Precision': 0.5253571428571429,
'Validation Recall scores': array([0.6 , 0.6 , 0.2 , 0.8 , 0.4 ,
1. , 0.33333333, 0.66666667, 0.6 , 0.8 ]),
'Mean Validation Recall': 0.5999999999999999,
'Validation F1 scores': array([0.5 , 0.5 , 0.2 , 0.72727273, 0.4 ,
0.76923077, 0.44444444, 0.61538462, 0.6 , 0.72727273]),
'Mean Validation F1 Score': 0.5483605283605283}
#y_E
svm = LinearSVC(max_iter=90000)
#perform cross validation with model
svm_result = cross_validation(svm, X_IES_random, y_E, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
The main results are
Mean Validation F1: 0.5953535353535353
Mean Validation Accuracy 60.44444444444444
{'Training Accuracy scores': array([0.68181818, 0.67045455, 0.68181818, 0.63636364, 0.75 ,
0.64772727, 0.63636364, 0.64772727, 0.69662921, 0.65168539]),
'Mean Training Accuracy': 67.00587334014301,
'Training Precision scores': array([0.70731707, 0.68085106, 0.69565217, 0.66666667, 0.76086957,
0.65306122, 0.68421053, 0.65957447, 0.72093023, 0.64705882]),
'Mean Training Precision': 0.6876191817775863,
'Training Recall scores': array([0.64444444, 0.69565217, 0.69565217, 0.60869565, 0.76086957,
0.69565217, 0.56521739, 0.67391304, 0.67391304, 0.7173913 ]),
'Mean Training Recall': 0.6731400966183575,
'Training F1 scores': array([0.6744186 , 0.68817204, 0.69565217, 0.63636364, 0.76086957,
0.67368421, 0.61904762, 0.66666667, 0.69662921, 0.68041237]),
'Mean Training F1 Score': 0.6791916104013757,
'Validation Accuracy scores': array([0.6 , 0.6 , 0.6 , 0.6 , 0.4 ,
0.6 , 0.5 , 0.7 , 0.55555556, 0.88888889]),
'Mean Validation Accuracy': 60.44444444444444,
'Validation Precision scores': array([0.66666667, 0.6 , 0.6 , 0.57142857, 0.4 ,
0.66666667, 0.5 , 0.75 , 0.66666667, 0.83333333]),
'Mean Validation Precision': 0.6254761904761905,
'Validation Recall scores': array([0.66666667, 0.6 , 0.6 , 0.8 , 0.4 ,
0.4 , 0.4 , 0.6 , 0.4 , 1. ]),
'Mean Validation Recall': 0.5866666666666667,
'Validation F1 scores': array([0.66666667, 0.6 , 0.6 , 0.66666667, 0.4 ,
0.5 , 0.44444444, 0.66666667, 0.5 , 0.90909091]),
'Mean Validation F1 Score': 0.5953535353535353}
2.2 IES + shuffled BOLD -> personality#
#y_A
svm = LinearSVC(max_iter=90000)
#perform cross validation with model
svm_result = cross_validation(svm, X_IES_BOLD_shuf, y_A, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
The main results are
Mean Validation F1: 0.5468181818181819
Mean Validation Accuracy 53.222222222222214
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
{'Training Accuracy scores': array([0.71590909, 0.78409091, 0.76136364, 0.80681818, 0.72727273,
0.71590909, 0.72727273, 0.77272727, 0.73033708, 0.7752809 ]),
'Mean Training Accuracy': 75.16981613891727,
'Training Precision scores': array([0.73809524, 0.7826087 , 0.77272727, 0.81818182, 0.75609756,
0.72727273, 0.75609756, 0.79069767, 0.73333333, 0.79069767]),
'Mean Training Precision': 0.7665809556050992,
'Training Recall scores': array([0.68888889, 0.8 , 0.75555556, 0.8 , 0.68888889,
0.71111111, 0.68888889, 0.75555556, 0.73333333, 0.75555556]),
'Mean Training Recall': 0.7377777777777778,
'Training F1 scores': array([0.71264368, 0.79120879, 0.76404494, 0.80898876, 0.72093023,
0.71910112, 0.72093023, 0.77272727, 0.73333333, 0.77272727]),
'Mean Training F1 Score': 0.7516635644734542,
'Validation Accuracy scores': array([0.8 , 0.5 , 0.5 , 0.5 , 0.7 ,
0.4 , 0.3 , 0.4 , 0.55555556, 0.66666667]),
'Mean Validation Accuracy': 53.222222222222214,
'Validation Precision scores': array([1. , 0.5 , 0.5 , 0.5 , 0.66666667,
0.4 , 0.25 , 0.42857143, 0.57142857, 0.75 ]),
'Mean Validation Precision': 0.5566666666666666,
'Validation Recall scores': array([0.6, 0.4, 0.6, 0.6, 0.8, 0.4, 0.2, 0.6, 0.8, 0.6]),
'Mean Validation Recall': 0.5599999999999999,
'Validation F1 scores': array([0.75 , 0.44444444, 0.54545455, 0.54545455, 0.72727273,
0.4 , 0.22222222, 0.5 , 0.66666667, 0.66666667]),
'Mean Validation F1 Score': 0.5468181818181819}
#y_O
svm = LinearSVC(max_iter=90000)
#perform cross validation with model
svm_result = cross_validation(svm, X_IES_BOLD_shuf, y_O, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
The main results are
Mean Validation F1: 0.4716666666666667
Mean Validation Accuracy 50.22222222222222
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
{'Training Accuracy scores': array([0.67045455, 0.68181818, 0.67045455, 0.64772727, 0.70454545,
0.70454545, 0.70454545, 0.61363636, 0.68539326, 0.66292135]),
'Mean Training Accuracy': 67.46041879468845,
'Training Precision scores': array([0.67391304, 0.70731707, 0.67391304, 0.66666667, 0.74358974,
0.72093023, 0.74358974, 0.62222222, 0.71794872, 0.69230769]),
'Mean Training Precision': 0.696239817901018,
'Training Recall scores': array([0.68888889, 0.64444444, 0.68888889, 0.62222222, 0.64444444,
0.68888889, 0.64444444, 0.62222222, 0.62222222, 0.6 ]),
'Mean Training Recall': 0.6466666666666667,
'Training F1 scores': array([0.68131868, 0.6744186 , 0.68131868, 0.64367816, 0.69047619,
0.70454545, 0.69047619, 0.62222222, 0.66666667, 0.64285714]),
'Mean Training F1 Score': 0.6697977995451934,
'Validation Accuracy scores': array([0.6 , 0.6 , 0.4 , 0.4 , 0.2 ,
0.5 , 0.3 , 0.8 , 0.55555556, 0.66666667]),
'Mean Validation Accuracy': 50.22222222222222,
'Validation Precision scores': array([0.57142857, 0.57142857, 0.33333333, 0.4 , 0. ,
0.5 , 0.25 , 0.8 , 0.6 , 0.75 ]),
'Mean Validation Precision': 0.4776190476190476,
'Validation Recall scores': array([0.8, 0.8, 0.2, 0.4, 0. , 0.4, 0.2, 0.8, 0.6, 0.6]),
'Mean Validation Recall': 0.48,
'Validation F1 scores': array([0.66666667, 0.66666667, 0.25 , 0.4 , 0. ,
0.44444444, 0.22222222, 0.8 , 0.6 , 0.66666667]),
'Mean Validation F1 Score': 0.4716666666666667}
#y_C
svm = LinearSVC(max_iter=90000)
#perform cross validation with model
svm_result = cross_validation(svm, X_IES_BOLD_shuf, y_C, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
The main results are
Mean Validation F1: 0.5663869463869464
Mean Validation Accuracy 51.77777777777778
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
{'Training Accuracy scores': array([0.68181818, 0.70454545, 0.69318182, 0.70454545, 0.70454545,
0.63636364, 0.64772727, 0.72727273, 0.70786517, 0.76404494]),
'Mean Training Accuracy': 69.71910112359551,
'Training Precision scores': array([0.6875 , 0.7173913 , 0.7 , 0.71428571, 0.71428571,
0.65957447, 0.65384615, 0.70909091, 0.72340426, 0.77083333]),
'Mean Training Precision': 0.7050211852593906,
'Training Recall scores': array([0.7173913 , 0.7173913 , 0.74468085, 0.74468085, 0.74468085,
0.65957447, 0.72340426, 0.82978723, 0.72340426, 0.78723404]),
'Mean Training Recall': 0.7392229417206291,
'Training F1 scores': array([0.70212766, 0.7173913 , 0.72164948, 0.72916667, 0.72916667,
0.65957447, 0.68686869, 0.76470588, 0.72340426, 0.77894737]),
'Mean Training F1 Score': 0.7213002442838645,
'Validation Accuracy scores': array([0.9 , 0.3 , 0.5 , 0.8 , 0.4 ,
0.5 , 0.4 , 0.6 , 0.55555556, 0.22222222]),
'Mean Validation Accuracy': 51.77777777777778,
'Validation Precision scores': array([1. , 0.4 , 0.5 , 0.8 , 0.4 ,
0.5 , 0.4 , 0.6 , 0.57142857, 0.33333333]),
'Mean Validation Precision': 0.5504761904761903,
'Validation Recall scores': array([0.83333333, 0.33333333, 0.6 , 0.8 , 0.4 ,
0.8 , 0.4 , 0.6 , 0.8 , 0.4 ]),
'Mean Validation Recall': 0.5966666666666667,
'Validation F1 scores': array([0.90909091, 0.36363636, 0.54545455, 0.8 , 0.4 ,
0.61538462, 0.4 , 0.6 , 0.66666667, 0.36363636]),
'Mean Validation F1 Score': 0.5663869463869464}
#y_N
svm = LinearSVC(max_iter=90000)
#perform cross validation with model
svm_result = cross_validation(svm, X_IES_BOLD_shuf, y_N, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
The main results are
Mean Validation F1: 0.5371212121212121
Mean Validation Accuracy 53.0
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
{'Training Accuracy scores': array([0.71590909, 0.67045455, 0.71590909, 0.75 , 0.75 ,
0.70454545, 0.65909091, 0.70454545, 0.71910112, 0.70786517]),
'Mean Training Accuracy': 70.97420837589377,
'Training Precision scores': array([0.73913043, 0.6875 , 0.72916667, 0.74509804, 0.76595745,
0.73333333, 0.66666667, 0.72727273, 0.73913043, 0.72340426]),
'Mean Training Precision': 0.7256660004847958,
'Training Recall scores': array([0.72340426, 0.70212766, 0.74468085, 0.80851064, 0.76595745,
0.70212766, 0.69565217, 0.69565217, 0.72340426, 0.72340426]),
'Mean Training Recall': 0.7284921369102684,
'Training F1 scores': array([0.7311828 , 0.69473684, 0.73684211, 0.7755102 , 0.76595745,
0.7173913 , 0.68085106, 0.71111111, 0.7311828 , 0.72340426]),
'Mean Training F1 Score': 0.7268169924264287,
'Validation Accuracy scores': array([0.4 , 0.7 , 0.5 , 0.5 , 0.5 ,
0.6 , 0.7 , 0.4 , 0.66666667, 0.33333333]),
'Mean Validation Accuracy': 53.0,
'Validation Precision scores': array([0.42857143, 0.66666667, 0.5 , 0.5 , 0.5 ,
0.57142857, 0.8 , 0.5 , 0.75 , 0.33333333]),
'Mean Validation Precision': 0.5549999999999999,
'Validation Recall scores': array([0.6 , 0.8 , 0.4 , 0.4 , 0.4 ,
0.8 , 0.66666667, 0.5 , 0.6 , 0.2 ]),
'Mean Validation Recall': 0.5366666666666666,
'Validation F1 scores': array([0.5 , 0.72727273, 0.44444444, 0.44444444, 0.44444444,
0.66666667, 0.72727273, 0.5 , 0.66666667, 0.25 ]),
'Mean Validation F1 Score': 0.5371212121212121}
#y_E
svm = LinearSVC(max_iter=90000)
#perform cross validation with model
svm_result = cross_validation(svm, X_IES_BOLD_shuf, y_E, num_folds)
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
svm_result
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
The main results are
Mean Validation F1: 0.5428421578421577
Mean Validation Accuracy 51.33333333333334
/usr/local/lib/python3.10/dist-packages/sklearn/svm/_base.py:1244: ConvergenceWarning: Liblinear failed to converge, increase the number of iterations.
warnings.warn(
{'Training Accuracy scores': array([0.65909091, 0.67045455, 0.69318182, 0.69318182, 0.70454545,
0.69318182, 0.68181818, 0.76136364, 0.68539326, 0.66292135]),
'Mean Training Accuracy': 69.05132788559754,
'Training Precision scores': array([0.65957447, 0.68085106, 0.69387755, 0.67924528, 0.69230769,
0.68627451, 0.68 , 0.75510204, 0.68 , 0.66666667]),
'Mean Training Precision': 0.6873899275548776,
'Training Recall scores': array([0.68888889, 0.69565217, 0.73913043, 0.7826087 , 0.7826087 ,
0.76086957, 0.73913043, 0.80434783, 0.73913043, 0.69565217]),
'Mean Training Recall': 0.7428019323671498,
'Training F1 scores': array([0.67391304, 0.68817204, 0.71578947, 0.72727273, 0.73469388,
0.72164948, 0.70833333, 0.77894737, 0.70833333, 0.68085106]),
'Mean Training F1 Score': 0.713795574845056,
'Validation Accuracy scores': array([0.5 , 0.6 , 0.4 , 0.3 , 0.3 ,
0.8 , 0.4 , 0.5 , 0.66666667, 0.66666667]),
'Mean Validation Accuracy': 51.33333333333334,
'Validation Precision scores': array([0.66666667, 0.6 , 0.42857143, 0.25 , 0.375 ,
1. , 0.44444444, 0.5 , 0.75 , 0.75 ]),
'Mean Validation Precision': 0.576468253968254,
'Validation Recall scores': array([0.33333333, 0.6 , 0.6 , 0.2 , 0.6 ,
0.6 , 0.8 , 0.6 , 0.6 , 0.6 ]),
'Mean Validation Recall': 0.5533333333333332,
'Validation F1 scores': array([0.44444444, 0.6 , 0.5 , 0.22222222, 0.46153846,
0.75 , 0.57142857, 0.54545455, 0.66666667, 0.66666667]),
'Mean Validation F1 Score': 0.5428421578421577}
Logistic Regression#
1.1 IES -> personality#
from sklearn.linear_model import LogisticRegression
#define the model
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
#y_A
logis_result = cross_validation(logis_reg_model, X_IES, y_A, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.6001554001554001
Mean Validation Accuracy 56.33333333333332
{'Training Accuracy scores': array([0.64772727, 0.67045455, 0.70454545, 0.64772727, 0.67045455,
0.69318182, 0.68181818, 0.65909091, 0.60674157, 0.64044944]),
'Mean Training Accuracy': 66.22191011235955,
'Training Precision scores': array([0.64583333, 0.65384615, 0.70212766, 0.65217391, 0.68181818,
0.6875 , 0.66666667, 0.66666667, 0.60416667, 0.63829787]),
'Mean Training Precision': 0.6599097113956041,
'Training Recall scores': array([0.68888889, 0.75555556, 0.73333333, 0.66666667, 0.66666667,
0.73333333, 0.75555556, 0.66666667, 0.64444444, 0.66666667]),
'Mean Training Recall': 0.6977777777777778,
'Training F1 scores': array([0.66666667, 0.70103093, 0.7173913 , 0.65934066, 0.6741573 ,
0.70967742, 0.70833333, 0.66666667, 0.62365591, 0.65217391]),
'Mean Training F1 Score': 0.6779094107937802,
'Validation Accuracy scores': array([0.6 , 0.5 , 0.3 , 0.5 , 0.7 ,
0.5 , 0.6 , 0.6 , 0.77777778, 0.55555556]),
'Mean Validation Accuracy': 56.33333333333332,
'Validation Precision scores': array([0.6 , 0.5 , 0.33333333, 0.5 , 0.625 ,
0.5 , 0.57142857, 0.57142857, 0.8 , 0.6 ]),
'Mean Validation Precision': 0.5601190476190475,
'Validation Recall scores': array([0.6, 0.4, 0.4, 0.6, 1. , 0.6, 0.8, 0.8, 0.8, 0.6]),
'Mean Validation Recall': 0.6599999999999999,
'Validation F1 scores': array([0.6 , 0.44444444, 0.36363636, 0.54545455, 0.76923077,
0.54545455, 0.66666667, 0.66666667, 0.8 , 0.6 ]),
'Mean Validation F1 Score': 0.6001554001554001}
#y_O
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES, y_O, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5536285936285936
Mean Validation Accuracy 52.33333333333333
{'Training Accuracy scores': array([0.57954545, 0.59090909, 0.59090909, 0.625 , 0.61363636,
0.56818182, 0.60227273, 0.55681818, 0.56179775, 0.5505618 ]),
'Mean Training Accuracy': 58.396322778345244,
'Training Precision scores': array([0.58695652, 0.58823529, 0.58823529, 0.61538462, 0.62790698,
0.58139535, 0.61363636, 0.55769231, 0.56521739, 0.55102041]),
'Mean Training Precision': 0.5875680521736719,
'Training Recall scores': array([0.6 , 0.66666667, 0.66666667, 0.71111111, 0.6 ,
0.55555556, 0.6 , 0.64444444, 0.57777778, 0.6 ]),
'Mean Training Recall': 0.6222222222222221,
'Training F1 scores': array([0.59340659, 0.625 , 0.625 , 0.65979381, 0.61363636,
0.56818182, 0.60674157, 0.59793814, 0.57142857, 0.57446809]),
'Mean Training F1 Score': 0.6035594963556323,
'Validation Accuracy scores': array([0.3 , 0.6 , 0.8 , 0.5 , 0.3 ,
0.4 , 0.4 , 0.6 , 0.77777778, 0.55555556]),
'Mean Validation Accuracy': 52.33333333333333,
'Validation Precision scores': array([0.375 , 0.66666667, 0.8 , 0.5 , 0.33333333,
0.42857143, 0.4 , 0.6 , 0.8 , 0.57142857]),
'Mean Validation Precision': 0.5475,
'Validation Recall scores': array([0.6, 0.4, 0.8, 0.4, 0.4, 0.6, 0.4, 0.6, 0.8, 0.8]),
'Mean Validation Recall': 0.58,
'Validation F1 scores': array([0.46153846, 0.5 , 0.8 , 0.44444444, 0.36363636,
0.5 , 0.4 , 0.6 , 0.8 , 0.66666667]),
'Mean Validation F1 Score': 0.5536285936285936}
#y_C
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES, y_C, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5348140748140748
Mean Validation Accuracy 43.88888888888889
{'Training Accuracy scores': array([0.57954545, 0.57954545, 0.61363636, 0.52272727, 0.54545455,
0.52272727, 0.59090909, 0.59090909, 0.58426966, 0.62921348]),
'Mean Training Accuracy': 57.5893769152196,
'Training Precision scores': array([0.57377049, 0.58181818, 0.60655738, 0.53731343, 0.55737705,
0.54385965, 0.60377358, 0.59322034, 0.58064516, 0.62068966]),
'Mean Training Precision': 0.5799024922161045,
'Training Recall scores': array([0.76086957, 0.69565217, 0.78723404, 0.76595745, 0.72340426,
0.65957447, 0.68085106, 0.74468085, 0.76595745, 0.76595745]),
'Mean Training Recall': 0.735013876040703,
'Training F1 scores': array([0.65420561, 0.63366337, 0.68518519, 0.63157895, 0.62962963,
0.59615385, 0.64 , 0.66037736, 0.66055046, 0.68571429]),
'Mean Training F1 Score': 0.6477058685070799,
'Validation Accuracy scores': array([0.6 , 0.2 , 0.4 , 0.6 , 0.4 ,
0.5 , 0.4 , 0.4 , 0.44444444, 0.44444444]),
'Mean Validation Accuracy': 43.88888888888889,
'Validation Precision scores': array([0.75 , 0.33333333, 0.42857143, 0.57142857, 0.44444444,
0.5 , 0.42857143, 0.44444444, 0.5 , 0.5 ]),
'Mean Validation Precision': 0.490079365079365,
'Validation Recall scores': array([0.5 , 0.33333333, 0.6 , 0.8 , 0.8 ,
0.8 , 0.6 , 0.8 , 0.4 , 0.6 ]),
'Mean Validation Recall': 0.6233333333333333,
'Validation F1 scores': array([0.6 , 0.33333333, 0.5 , 0.66666667, 0.57142857,
0.61538462, 0.5 , 0.57142857, 0.44444444, 0.54545455]),
'Mean Validation F1 Score': 0.5348140748140748}
#y_N
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES, y_N, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5056277056277056
Mean Validation Accuracy 48.111111111111114
{'Training Accuracy scores': array([0.60227273, 0.60227273, 0.57954545, 0.61363636, 0.59090909,
0.60227273, 0.61363636, 0.61363636, 0.60674157, 0.58426966]),
'Mean Training Accuracy': 60.09193054136874,
'Training Precision scores': array([0.625 , 0.62 , 0.59615385, 0.63265306, 0.61702128,
0.63043478, 0.63043478, 0.63043478, 0.625 , 0.59615385]),
'Mean Training Precision': 0.6203286377954014,
'Training Recall scores': array([0.63829787, 0.65957447, 0.65957447, 0.65957447, 0.61702128,
0.61702128, 0.63043478, 0.63043478, 0.63829787, 0.65957447]),
'Mean Training Recall': 0.6409805735430156,
'Training F1 scores': array([0.63157895, 0.63917526, 0.62626263, 0.64583333, 0.61702128,
0.62365591, 0.63043478, 0.63043478, 0.63157895, 0.62626263]),
'Mean Training F1 Score': 0.6302238494119017,
'Validation Accuracy scores': array([0.5 , 0.4 , 0.3 , 0.5 , 0.6 ,
0.4 , 0.6 , 0.4 , 0.44444444, 0.66666667]),
'Mean Validation Accuracy': 48.111111111111114,
'Validation Precision scores': array([0.5 , 0.42857143, 0.25 , 0.5 , 0.66666667,
0.44444444, 1. , 0.5 , 0.5 , 0.66666667]),
'Mean Validation Precision': 0.5456349206349207,
'Validation Recall scores': array([0.6 , 0.6 , 0.2 , 0.6 , 0.4 ,
0.8 , 0.33333333, 0.5 , 0.4 , 0.8 ]),
'Mean Validation Recall': 0.5233333333333333,
'Validation F1 scores': array([0.54545455, 0.5 , 0.22222222, 0.54545455, 0.5 ,
0.57142857, 0.5 , 0.5 , 0.44444444, 0.72727273]),
'Mean Validation F1 Score': 0.5056277056277056}
#y_E
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES, y_E, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5864657564657565
Mean Validation Accuracy 52.22222222222223
{'Training Accuracy scores': array([0.60227273, 0.57954545, 0.625 , 0.60227273, 0.63636364,
0.59090909, 0.55681818, 0.625 , 0.59550562, 0.62921348]),
'Mean Training Accuracy': 60.42900919305414,
'Training Precision scores': array([0.59259259, 0.57627119, 0.61016949, 0.59322034, 0.625 ,
0.59615385, 0.55737705, 0.62264151, 0.58928571, 0.61403509]),
'Mean Training Precision': 0.5976746816314893,
'Training Recall scores': array([0.71111111, 0.73913043, 0.7826087 , 0.76086957, 0.76086957,
0.67391304, 0.73913043, 0.7173913 , 0.7173913 , 0.76086957]),
'Mean Training Recall': 0.736328502415459,
'Training F1 scores': array([0.64646465, 0.64761905, 0.68571429, 0.66666667, 0.68627451,
0.63265306, 0.63551402, 0.66666667, 0.64705882, 0.67961165]),
'Mean Training F1 Score': 0.6594243376866162,
'Validation Accuracy scores': array([0.7 , 0.6 , 0.3 , 0.3 , 0.4 ,
0.6 , 0.6 , 0.5 , 0.77777778, 0.44444444]),
'Mean Validation Accuracy': 52.22222222222223,
'Validation Precision scores': array([0.8 , 0.57142857, 0.375 , 0.33333333, 0.44444444,
0.66666667, 0.55555556, 0.5 , 0.8 , 0.5 ]),
'Mean Validation Precision': 0.5546428571428572,
'Validation Recall scores': array([0.66666667, 0.8 , 0.6 , 0.4 , 0.8 ,
0.4 , 1. , 0.8 , 0.8 , 0.4 ]),
'Mean Validation Recall': 0.6666666666666667,
'Validation F1 scores': array([0.72727273, 0.66666667, 0.46153846, 0.36363636, 0.57142857,
0.5 , 0.71428571, 0.61538462, 0.8 , 0.44444444]),
'Mean Validation F1 Score': 0.5864657564657565}
1.2 IES + relevant BOLD -> personality#
#y_A
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_combined, y_A, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5623232323232324
Mean Validation Accuracy 54.33333333333334
{'Training Accuracy scores': array([0.72727273, 0.76136364, 0.76136364, 0.81818182, 0.72727273,
0.70454545, 0.71590909, 0.77272727, 0.73033708, 0.76404494]),
'Mean Training Accuracy': 74.83018386108274,
'Training Precision scores': array([0.73333333, 0.76086957, 0.75 , 0.8372093 , 0.75609756,
0.72093023, 0.73809524, 0.77777778, 0.73333333, 0.78571429]),
'Mean Training Precision': 0.759336062933069,
'Training Recall scores': array([0.73333333, 0.77777778, 0.8 , 0.8 , 0.68888889,
0.68888889, 0.68888889, 0.77777778, 0.73333333, 0.73333333]),
'Mean Training Recall': 0.7422222222222222,
'Training F1 scores': array([0.73333333, 0.76923077, 0.77419355, 0.81818182, 0.72093023,
0.70454545, 0.71264368, 0.77777778, 0.73333333, 0.75862069]),
'Mean Training F1 Score': 0.7502790635163815,
'Validation Accuracy scores': array([0.9 , 0.3 , 0.5 , 0.5 , 0.7 ,
0.4 , 0.4 , 0.4 , 0.66666667, 0.66666667]),
'Mean Validation Accuracy': 54.33333333333334,
'Validation Precision scores': array([1. , 0.25 , 0.5 , 0.5 , 0.66666667,
0.4 , 0.4 , 0.42857143, 0.66666667, 0.75 ]),
'Mean Validation Precision': 0.5561904761904762,
'Validation Recall scores': array([0.8, 0.2, 0.6, 0.6, 0.8, 0.4, 0.4, 0.6, 0.8, 0.6]),
'Mean Validation Recall': 0.58,
'Validation F1 scores': array([0.88888889, 0.22222222, 0.54545455, 0.54545455, 0.72727273,
0.4 , 0.4 , 0.5 , 0.72727273, 0.66666667]),
'Mean Validation F1 Score': 0.5623232323232324}
#y_O
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_combined, y_O, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.4307575757575758
Mean Validation Accuracy 47.0
{'Training Accuracy scores': array([0.63636364, 0.68181818, 0.69318182, 0.67045455, 0.71590909,
0.71590909, 0.73863636, 0.65909091, 0.66292135, 0.66292135]),
'Mean Training Accuracy': 68.3720633299285,
'Training Precision scores': array([0.63265306, 0.70731707, 0.69565217, 0.67391304, 0.73809524,
0.72727273, 0.76190476, 0.65957447, 0.6744186 , 0.6744186 ]),
'Mean Training Precision': 0.6945219756446686,
'Training Recall scores': array([0.68888889, 0.64444444, 0.71111111, 0.68888889, 0.68888889,
0.71111111, 0.71111111, 0.68888889, 0.64444444, 0.64444444]),
'Mean Training Recall': 0.6822222222222223,
'Training F1 scores': array([0.65957447, 0.6744186 , 0.7032967 , 0.68131868, 0.71264368,
0.71910112, 0.73563218, 0.67391304, 0.65909091, 0.65909091]),
'Mean Training F1 Score': 0.6878080304676203,
'Validation Accuracy scores': array([0.5 , 0.6 , 0.2 , 0.4 , 0.2 ,
0.6 , 0.4 , 0.8 , 0.44444444, 0.55555556]),
'Mean Validation Accuracy': 47.0,
'Validation Precision scores': array([0.5 , 0.57142857, 0. , 0.4 , 0. ,
0.66666667, 0.33333333, 0.8 , 0.5 , 0.6 ]),
'Mean Validation Precision': 0.4371428571428571,
'Validation Recall scores': array([0.6, 0.8, 0. , 0.4, 0. , 0.4, 0.2, 0.8, 0.6, 0.6]),
'Mean Validation Recall': 0.43999999999999995,
'Validation F1 scores': array([0.54545455, 0.66666667, 0. , 0.4 , 0. ,
0.5 , 0.25 , 0.8 , 0.54545455, 0.6 ]),
'Mean Validation F1 Score': 0.4307575757575758}
#y_C
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_combined, y_C, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5800233100233101
Mean Validation Accuracy 52.888888888888886
{'Training Accuracy scores': array([0.65909091, 0.69318182, 0.70454545, 0.70454545, 0.70454545,
0.64772727, 0.68181818, 0.71590909, 0.70786517, 0.74157303]),
'Mean Training Accuracy': 69.60801838610827,
'Training Precision scores': array([0.66666667, 0.71111111, 0.71428571, 0.71428571, 0.71428571,
0.66666667, 0.68627451, 0.69642857, 0.72340426, 0.75 ]),
'Mean Training Precision': 0.7043408923853229,
'Training Recall scores': array([0.69565217, 0.69565217, 0.74468085, 0.74468085, 0.74468085,
0.68085106, 0.74468085, 0.82978723, 0.72340426, 0.76595745]),
'Mean Training Recall': 0.7370027752081406,
'Training F1 scores': array([0.68085106, 0.7032967 , 0.72916667, 0.72916667, 0.72916667,
0.67368421, 0.71428571, 0.75728155, 0.72340426, 0.75789474]),
'Mean Training F1 Score': 0.7198198237497834,
'Validation Accuracy scores': array([0.9 , 0.3 , 0.5 , 0.8 , 0.4 ,
0.5 , 0.4 , 0.6 , 0.55555556, 0.33333333]),
'Mean Validation Accuracy': 52.888888888888886,
'Validation Precision scores': array([1. , 0.4 , 0.5 , 0.8 , 0.4 ,
0.5 , 0.4 , 0.6 , 0.57142857, 0.42857143]),
'Mean Validation Precision': 0.5599999999999999,
'Validation Recall scores': array([0.83333333, 0.33333333, 0.6 , 0.8 , 0.4 ,
0.8 , 0.4 , 0.6 , 0.8 , 0.6 ]),
'Mean Validation Recall': 0.6166666666666666,
'Validation F1 scores': array([0.90909091, 0.36363636, 0.54545455, 0.8 , 0.4 ,
0.61538462, 0.4 , 0.6 , 0.66666667, 0.5 ]),
'Mean Validation F1 Score': 0.5800233100233101}
#y_N
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_combined, y_N, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5598484848484848
Mean Validation Accuracy 55.00000000000001
{'Training Accuracy scores': array([0.69318182, 0.67045455, 0.70454545, 0.76136364, 0.73863636,
0.70454545, 0.67045455, 0.73863636, 0.68539326, 0.73033708]),
'Mean Training Accuracy': 70.97548518896834,
'Training Precision scores': array([0.7 , 0.6875 , 0.71428571, 0.76 , 0.74 ,
0.71428571, 0.68085106, 0.74468085, 0.71111111, 0.74468085]),
'Mean Training Precision': 0.7197395305639986,
'Training Recall scores': array([0.74468085, 0.70212766, 0.74468085, 0.80851064, 0.78723404,
0.74468085, 0.69565217, 0.76086957, 0.68085106, 0.74468085]),
'Mean Training Recall': 0.7413968547641073,
'Training F1 scores': array([0.72164948, 0.69473684, 0.72916667, 0.78350515, 0.7628866 ,
0.72916667, 0.68817204, 0.75268817, 0.69565217, 0.74468085]),
'Mean Training F1 Score': 0.7302304652582635,
'Validation Accuracy scores': array([0.4 , 0.7 , 0.5 , 0.5 , 0.5 ,
0.5 , 0.9 , 0.5 , 0.66666667, 0.33333333]),
'Mean Validation Accuracy': 55.00000000000001,
'Validation Precision scores': array([0.42857143, 0.66666667, 0.5 , 0.5 , 0.5 ,
0.5 , 1. , 0.55555556, 0.75 , 0.33333333]),
'Mean Validation Precision': 0.5734126984126984,
'Validation Recall scores': array([0.6 , 0.8 , 0.4 , 0.4 , 0.4 ,
0.6 , 0.83333333, 0.83333333, 0.6 , 0.2 ]),
'Mean Validation Recall': 0.5666666666666667,
'Validation F1 scores': array([0.5 , 0.72727273, 0.44444444, 0.44444444, 0.44444444,
0.54545455, 0.90909091, 0.66666667, 0.66666667, 0.25 ]),
'Mean Validation F1 Score': 0.5598484848484848}
#y_E
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_combined, y_E, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5271855921855921
Mean Validation Accuracy 50.22222222222222
{'Training Accuracy scores': array([0.64772727, 0.65909091, 0.69318182, 0.70454545, 0.67045455,
0.67045455, 0.68181818, 0.76136364, 0.66292135, 0.6741573 ]),
'Mean Training Accuracy': 68.25715015321757,
'Training Precision scores': array([0.65217391, 0.67391304, 0.68627451, 0.69230769, 0.68085106,
0.67346939, 0.68 , 0.76595745, 0.66 , 0.66666667]),
'Mean Training Precision': 0.6831613723693419,
'Training Recall scores': array([0.66666667, 0.67391304, 0.76086957, 0.7826087 , 0.69565217,
0.7173913 , 0.73913043, 0.7826087 , 0.7173913 , 0.73913043]),
'Mean Training Recall': 0.727536231884058,
'Training F1 scores': array([0.65934066, 0.67391304, 0.72164948, 0.73469388, 0.68817204,
0.69473684, 0.70833333, 0.77419355, 0.6875 , 0.70103093]),
'Mean Training F1 Score': 0.704356375957752,
'Validation Accuracy scores': array([0.4 , 0.6 , 0.4 , 0.3 , 0.3 ,
0.8 , 0.4 , 0.6 , 0.66666667, 0.55555556]),
'Mean Validation Accuracy': 50.22222222222222,
'Validation Precision scores': array([0.5 , 0.6 , 0.42857143, 0.25 , 0.375 ,
1. , 0.44444444, 0.6 , 0.75 , 0.66666667]),
'Mean Validation Precision': 0.561468253968254,
'Validation Recall scores': array([0.33333333, 0.6 , 0.6 , 0.2 , 0.6 ,
0.6 , 0.8 , 0.6 , 0.6 , 0.4 ]),
'Mean Validation Recall': 0.5333333333333333,
'Validation F1 scores': array([0.4 , 0.6 , 0.5 , 0.22222222, 0.46153846,
0.75 , 0.57142857, 0.6 , 0.66666667, 0.5 ]),
'Mean Validation F1 Score': 0.5271855921855921}
2.1 shuffled IES -> personality#
#y_A
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES_random, y_A, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5549728049728049
Mean Validation Accuracy 52.77777777777778
{'Training Accuracy scores': array([0.56818182, 0.57954545, 0.61363636, 0.55681818, 0.56818182,
0.57954545, 0.57954545, 0.55681818, 0.59550562, 0.57303371]),
'Mean Training Accuracy': 57.708120531154236,
'Training Precision scores': array([0.56603774, 0.57692308, 0.61702128, 0.55172414, 0.57142857,
0.57142857, 0.58 , 0.55769231, 0.59574468, 0.56862745]),
'Mean Training Precision': 0.5756627809679818,
'Training Recall scores': array([0.66666667, 0.66666667, 0.64444444, 0.71111111, 0.62222222,
0.71111111, 0.64444444, 0.64444444, 0.62222222, 0.64444444]),
'Mean Training Recall': 0.6577777777777778,
'Training F1 scores': array([0.6122449 , 0.6185567 , 0.63043478, 0.62135922, 0.59574468,
0.63366337, 0.61052632, 0.59793814, 0.60869565, 0.60416667]),
'Mean Training F1 Score': 0.6133330431047426,
'Validation Accuracy scores': array([0.5 , 0.6 , 0.5 , 0.6 , 0.6 ,
0.6 , 0.5 , 0.6 , 0.44444444, 0.33333333]),
'Mean Validation Accuracy': 52.77777777777778,
'Validation Precision scores': array([0.5 , 0.57142857, 0.5 , 0.6 , 0.57142857,
0.66666667, 0.5 , 0.57142857, 0.5 , 0.4 ]),
'Mean Validation Precision': 0.5380952380952382,
'Validation Recall scores': array([0.4, 0.8, 0.4, 0.6, 0.8, 0.4, 0.8, 0.8, 0.6, 0.4]),
'Mean Validation Recall': 0.6,
'Validation F1 scores': array([0.44444444, 0.66666667, 0.44444444, 0.6 , 0.66666667,
0.5 , 0.61538462, 0.66666667, 0.54545455, 0.4 ]),
'Mean Validation F1 Score': 0.5549728049728049}
#y_O
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES_random, y_O, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5517782217782219
Mean Validation Accuracy 50.0
{'Training Accuracy scores': array([0.64772727, 0.59090909, 0.56818182, 0.60227273, 0.59090909,
0.61363636, 0.625 , 0.64772727, 0.5505618 , 0.58426966]),
'Mean Training Accuracy': 60.211950970377934,
'Training Precision scores': array([0.64 , 0.58490566, 0.56363636, 0.59259259, 0.58823529,
0.61702128, 0.61538462, 0.63461538, 0.54901961, 0.58333333]),
'Mean Training Precision': 0.5968744128496176,
'Training Recall scores': array([0.71111111, 0.68888889, 0.68888889, 0.71111111, 0.66666667,
0.64444444, 0.71111111, 0.73333333, 0.62222222, 0.62222222]),
'Mean Training Recall': 0.6799999999999999,
'Training F1 scores': array([0.67368421, 0.63265306, 0.62 , 0.64646465, 0.625 ,
0.63043478, 0.65979381, 0.68041237, 0.58333333, 0.60215054]),
'Mean Training F1 Score': 0.6353926757358901,
'Validation Accuracy scores': array([0.5 , 0.6 , 0.5 , 0.3 , 0.6 ,
0.4 , 0.8 , 0.3 , 0.55555556, 0.44444444]),
'Mean Validation Accuracy': 50.0,
'Validation Precision scores': array([0.5 , 0.6 , 0.5 , 0.33333333, 0.66666667,
0.4 , 0.8 , 0.33333333, 0.55555556, 0.5 ]),
'Mean Validation Precision': 0.518888888888889,
'Validation Recall scores': array([0.8, 0.6, 0.6, 0.4, 0.4, 0.4, 0.8, 0.4, 1. , 0.8]),
'Mean Validation Recall': 0.62,
'Validation F1 scores': array([0.61538462, 0.6 , 0.54545455, 0.36363636, 0.5 ,
0.4 , 0.8 , 0.36363636, 0.71428571, 0.61538462]),
'Mean Validation F1 Score': 0.5517782217782219}
#y_C
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES_random, y_C, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.47019813519813525
Mean Validation Accuracy 42.8888888888889
{'Training Accuracy scores': array([0.59090909, 0.55681818, 0.55681818, 0.53409091, 0.48863636,
0.59090909, 0.57954545, 0.54545455, 0.56179775, 0.56179775]),
'Mean Training Accuracy': 55.66777323799796,
'Training Precision scores': array([0.59259259, 0.57142857, 0.57407407, 0.55769231, 0.51785714,
0.60377358, 0.59615385, 0.56140351, 0.57407407, 0.57692308]),
'Mean Training Precision': 0.5725972779473276,
'Training Recall scores': array([0.69565217, 0.60869565, 0.65957447, 0.61702128, 0.61702128,
0.68085106, 0.65957447, 0.68085106, 0.65957447, 0.63829787]),
'Mean Training Recall': 0.6517113783533764,
'Training F1 scores': array([0.64 , 0.58947368, 0.61386139, 0.58585859, 0.5631068 ,
0.64 , 0.62626263, 0.61538462, 0.61386139, 0.60606061]),
'Mean Training F1 Score': 0.6093869686170692,
'Validation Accuracy scores': array([0.2 , 0.5 , 0.5 , 0.5 , 0.5 ,
0.3 , 0.5 , 0.4 , 0.33333333, 0.55555556]),
'Mean Validation Accuracy': 42.8888888888889,
'Validation Precision scores': array([0.25 , 0.57142857, 0.5 , 0.5 , 0.5 ,
0.33333333, 0.5 , 0.33333333, 0.4 , 0.66666667]),
'Mean Validation Precision': 0.4554761904761905,
'Validation Recall scores': array([0.16666667, 0.66666667, 0.6 , 0.6 , 1. ,
0.4 , 0.8 , 0.2 , 0.4 , 0.4 ]),
'Mean Validation Recall': 0.5233333333333334,
'Validation F1 scores': array([0.2 , 0.61538462, 0.54545455, 0.54545455, 0.66666667,
0.36363636, 0.61538462, 0.25 , 0.4 , 0.5 ]),
'Mean Validation F1 Score': 0.47019813519813525}
#y_N
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES_random, y_N, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5247585747585748
Mean Validation Accuracy 44.666666666666664
{'Training Accuracy scores': array([0.61363636, 0.54545455, 0.59090909, 0.55681818, 0.64772727,
0.54545455, 0.56818182, 0.57954545, 0.70786517, 0.60674157]),
'Mean Training Accuracy': 59.623340143003055,
'Training Precision scores': array([0.61818182, 0.56140351, 0.59649123, 0.56896552, 0.62903226,
0.55555556, 0.57142857, 0.57894737, 0.67213115, 0.59677419]),
'Mean Training Precision': 0.5948911166824369,
'Training Recall scores': array([0.72340426, 0.68085106, 0.72340426, 0.70212766, 0.82978723,
0.74468085, 0.69565217, 0.7173913 , 0.87234043, 0.78723404]),
'Mean Training Recall': 0.7476873265494912,
'Training F1 scores': array([0.66666667, 0.61538462, 0.65384615, 0.62857143, 0.71559633,
0.63636364, 0.62745098, 0.6407767 , 0.75925926, 0.67889908]),
'Mean Training F1 Score': 0.662281485235708,
'Validation Accuracy scores': array([0.4 , 0.6 , 0.3 , 0.5 , 0.5 ,
0.4 , 0.7 , 0.4 , 0.11111111, 0.55555556]),
'Mean Validation Accuracy': 44.666666666666664,
'Validation Precision scores': array([0.44444444, 0.57142857, 0.33333333, 0.5 , 0.5 ,
0.42857143, 0.71428571, 0.5 , 0. , 0.55555556]),
'Mean Validation Precision': 0.45476190476190476,
'Validation Recall scores': array([0.8 , 0.8 , 0.4 , 0.6 , 0.6 ,
0.6 , 0.83333333, 0.66666667, 0. , 1. ]),
'Mean Validation Recall': 0.6300000000000001,
'Validation F1 scores': array([0.57142857, 0.66666667, 0.36363636, 0.54545455, 0.54545455,
0.5 , 0.76923077, 0.57142857, 0. , 0.71428571]),
'Mean Validation F1 Score': 0.5247585747585748}
#y_E
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES_random, y_E, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5758008658008658
Mean Validation Accuracy 54.22222222222223
{'Training Accuracy scores': array([0.625 , 0.625 , 0.63636364, 0.57954545, 0.63636364,
0.61363636, 0.67045455, 0.65909091, 0.59550562, 0.61797753]),
'Mean Training Accuracy': 62.58937691521961,
'Training Precision scores': array([0.63043478, 0.63265306, 0.64 , 0.58823529, 0.65217391,
0.625 , 0.67346939, 0.67391304, 0.6 , 0.63043478]),
'Mean Training Precision': 0.6346314264836368,
'Training Recall scores': array([0.64444444, 0.67391304, 0.69565217, 0.65217391, 0.65217391,
0.65217391, 0.7173913 , 0.67391304, 0.65217391, 0.63043478]),
'Mean Training Recall': 0.6644444444444444,
'Training F1 scores': array([0.63736264, 0.65263158, 0.66666667, 0.6185567 , 0.65217391,
0.63829787, 0.69473684, 0.67391304, 0.625 , 0.63043478]),
'Mean Training F1 Score': 0.6489774037583723,
'Validation Accuracy scores': array([0.5 , 0.6 , 0.6 , 0.7 , 0.4 ,
0.6 , 0.3 , 0.5 , 0.55555556, 0.66666667]),
'Mean Validation Accuracy': 54.22222222222223,
'Validation Precision scores': array([0.6 , 0.6 , 0.57142857, 0.66666667, 0.44444444,
0.57142857, 0.33333333, 0.5 , 0.66666667, 1. ]),
'Mean Validation Precision': 0.5953968253968254,
'Validation Recall scores': array([0.5, 0.6, 0.8, 0.8, 0.8, 0.8, 0.4, 0.6, 0.4, 0.4]),
'Mean Validation Recall': 0.6100000000000001,
'Validation F1 scores': array([0.54545455, 0.6 , 0.66666667, 0.72727273, 0.57142857,
0.66666667, 0.36363636, 0.54545455, 0.5 , 0.57142857]),
'Mean Validation F1 Score': 0.5758008658008658}
2.2 IES + shuffled BOLD -> personality#
#y_A
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES_BOLD_shuf, y_A, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5623232323232324
Mean Validation Accuracy 54.33333333333334
{'Training Accuracy scores': array([0.72727273, 0.76136364, 0.76136364, 0.81818182, 0.72727273,
0.70454545, 0.71590909, 0.77272727, 0.73033708, 0.76404494]),
'Mean Training Accuracy': 74.83018386108274,
'Training Precision scores': array([0.73333333, 0.76086957, 0.75 , 0.8372093 , 0.75609756,
0.72093023, 0.73809524, 0.77777778, 0.73333333, 0.78571429]),
'Mean Training Precision': 0.759336062933069,
'Training Recall scores': array([0.73333333, 0.77777778, 0.8 , 0.8 , 0.68888889,
0.68888889, 0.68888889, 0.77777778, 0.73333333, 0.73333333]),
'Mean Training Recall': 0.7422222222222222,
'Training F1 scores': array([0.73333333, 0.76923077, 0.77419355, 0.81818182, 0.72093023,
0.70454545, 0.71264368, 0.77777778, 0.73333333, 0.75862069]),
'Mean Training F1 Score': 0.7502790635163815,
'Validation Accuracy scores': array([0.9 , 0.3 , 0.5 , 0.5 , 0.7 ,
0.4 , 0.4 , 0.4 , 0.66666667, 0.66666667]),
'Mean Validation Accuracy': 54.33333333333334,
'Validation Precision scores': array([1. , 0.25 , 0.5 , 0.5 , 0.66666667,
0.4 , 0.4 , 0.42857143, 0.66666667, 0.75 ]),
'Mean Validation Precision': 0.5561904761904762,
'Validation Recall scores': array([0.8, 0.2, 0.6, 0.6, 0.8, 0.4, 0.4, 0.6, 0.8, 0.6]),
'Mean Validation Recall': 0.58,
'Validation F1 scores': array([0.88888889, 0.22222222, 0.54545455, 0.54545455, 0.72727273,
0.4 , 0.4 , 0.5 , 0.72727273, 0.66666667]),
'Mean Validation F1 Score': 0.5623232323232324}
#y_O
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES_BOLD_shuf, y_O, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.4307575757575758
Mean Validation Accuracy 47.0
{'Training Accuracy scores': array([0.63636364, 0.68181818, 0.69318182, 0.67045455, 0.71590909,
0.71590909, 0.73863636, 0.65909091, 0.66292135, 0.66292135]),
'Mean Training Accuracy': 68.3720633299285,
'Training Precision scores': array([0.63265306, 0.70731707, 0.69565217, 0.67391304, 0.73809524,
0.72727273, 0.76190476, 0.65957447, 0.6744186 , 0.6744186 ]),
'Mean Training Precision': 0.6945219756446686,
'Training Recall scores': array([0.68888889, 0.64444444, 0.71111111, 0.68888889, 0.68888889,
0.71111111, 0.71111111, 0.68888889, 0.64444444, 0.64444444]),
'Mean Training Recall': 0.6822222222222223,
'Training F1 scores': array([0.65957447, 0.6744186 , 0.7032967 , 0.68131868, 0.71264368,
0.71910112, 0.73563218, 0.67391304, 0.65909091, 0.65909091]),
'Mean Training F1 Score': 0.6878080304676203,
'Validation Accuracy scores': array([0.5 , 0.6 , 0.2 , 0.4 , 0.2 ,
0.6 , 0.4 , 0.8 , 0.44444444, 0.55555556]),
'Mean Validation Accuracy': 47.0,
'Validation Precision scores': array([0.5 , 0.57142857, 0. , 0.4 , 0. ,
0.66666667, 0.33333333, 0.8 , 0.5 , 0.6 ]),
'Mean Validation Precision': 0.4371428571428571,
'Validation Recall scores': array([0.6, 0.8, 0. , 0.4, 0. , 0.4, 0.2, 0.8, 0.6, 0.6]),
'Mean Validation Recall': 0.43999999999999995,
'Validation F1 scores': array([0.54545455, 0.66666667, 0. , 0.4 , 0. ,
0.5 , 0.25 , 0.8 , 0.54545455, 0.6 ]),
'Mean Validation F1 Score': 0.4307575757575758}
#y_C
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES_BOLD_shuf, y_O, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.4307575757575758
Mean Validation Accuracy 47.0
{'Training Accuracy scores': array([0.63636364, 0.68181818, 0.69318182, 0.67045455, 0.71590909,
0.71590909, 0.73863636, 0.65909091, 0.66292135, 0.66292135]),
'Mean Training Accuracy': 68.3720633299285,
'Training Precision scores': array([0.63265306, 0.70731707, 0.69565217, 0.67391304, 0.73809524,
0.72727273, 0.76190476, 0.65957447, 0.6744186 , 0.6744186 ]),
'Mean Training Precision': 0.6945219756446686,
'Training Recall scores': array([0.68888889, 0.64444444, 0.71111111, 0.68888889, 0.68888889,
0.71111111, 0.71111111, 0.68888889, 0.64444444, 0.64444444]),
'Mean Training Recall': 0.6822222222222223,
'Training F1 scores': array([0.65957447, 0.6744186 , 0.7032967 , 0.68131868, 0.71264368,
0.71910112, 0.73563218, 0.67391304, 0.65909091, 0.65909091]),
'Mean Training F1 Score': 0.6878080304676203,
'Validation Accuracy scores': array([0.5 , 0.6 , 0.2 , 0.4 , 0.2 ,
0.6 , 0.4 , 0.8 , 0.44444444, 0.55555556]),
'Mean Validation Accuracy': 47.0,
'Validation Precision scores': array([0.5 , 0.57142857, 0. , 0.4 , 0. ,
0.66666667, 0.33333333, 0.8 , 0.5 , 0.6 ]),
'Mean Validation Precision': 0.4371428571428571,
'Validation Recall scores': array([0.6, 0.8, 0. , 0.4, 0. , 0.4, 0.2, 0.8, 0.6, 0.6]),
'Mean Validation Recall': 0.43999999999999995,
'Validation F1 scores': array([0.54545455, 0.66666667, 0. , 0.4 , 0. ,
0.5 , 0.25 , 0.8 , 0.54545455, 0.6 ]),
'Mean Validation F1 Score': 0.4307575757575758}
#y_N
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES_BOLD_shuf, y_N, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5598484848484848
Mean Validation Accuracy 55.00000000000001
{'Training Accuracy scores': array([0.69318182, 0.67045455, 0.70454545, 0.76136364, 0.73863636,
0.70454545, 0.67045455, 0.73863636, 0.68539326, 0.73033708]),
'Mean Training Accuracy': 70.97548518896834,
'Training Precision scores': array([0.7 , 0.6875 , 0.71428571, 0.76 , 0.74 ,
0.71428571, 0.68085106, 0.74468085, 0.71111111, 0.74468085]),
'Mean Training Precision': 0.7197395305639986,
'Training Recall scores': array([0.74468085, 0.70212766, 0.74468085, 0.80851064, 0.78723404,
0.74468085, 0.69565217, 0.76086957, 0.68085106, 0.74468085]),
'Mean Training Recall': 0.7413968547641073,
'Training F1 scores': array([0.72164948, 0.69473684, 0.72916667, 0.78350515, 0.7628866 ,
0.72916667, 0.68817204, 0.75268817, 0.69565217, 0.74468085]),
'Mean Training F1 Score': 0.7302304652582635,
'Validation Accuracy scores': array([0.4 , 0.7 , 0.5 , 0.5 , 0.5 ,
0.5 , 0.9 , 0.5 , 0.66666667, 0.33333333]),
'Mean Validation Accuracy': 55.00000000000001,
'Validation Precision scores': array([0.42857143, 0.66666667, 0.5 , 0.5 , 0.5 ,
0.5 , 1. , 0.55555556, 0.75 , 0.33333333]),
'Mean Validation Precision': 0.5734126984126984,
'Validation Recall scores': array([0.6 , 0.8 , 0.4 , 0.4 , 0.4 ,
0.6 , 0.83333333, 0.83333333, 0.6 , 0.2 ]),
'Mean Validation Recall': 0.5666666666666667,
'Validation F1 scores': array([0.5 , 0.72727273, 0.44444444, 0.44444444, 0.44444444,
0.54545455, 0.90909091, 0.66666667, 0.66666667, 0.25 ]),
'Mean Validation F1 Score': 0.5598484848484848}
#y_E
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES_BOLD_shuf, y_E, num_folds)
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
logis_result
The main results are
Mean Validation F1: 0.5271855921855921
Mean Validation Accuracy 50.22222222222222
{'Training Accuracy scores': array([0.64772727, 0.65909091, 0.69318182, 0.70454545, 0.67045455,
0.67045455, 0.68181818, 0.76136364, 0.66292135, 0.6741573 ]),
'Mean Training Accuracy': 68.25715015321757,
'Training Precision scores': array([0.65217391, 0.67391304, 0.68627451, 0.69230769, 0.68085106,
0.67346939, 0.68 , 0.76595745, 0.66 , 0.66666667]),
'Mean Training Precision': 0.6831613723693419,
'Training Recall scores': array([0.66666667, 0.67391304, 0.76086957, 0.7826087 , 0.69565217,
0.7173913 , 0.73913043, 0.7826087 , 0.7173913 , 0.73913043]),
'Mean Training Recall': 0.727536231884058,
'Training F1 scores': array([0.65934066, 0.67391304, 0.72164948, 0.73469388, 0.68817204,
0.69473684, 0.70833333, 0.77419355, 0.6875 , 0.70103093]),
'Mean Training F1 Score': 0.704356375957752,
'Validation Accuracy scores': array([0.4 , 0.6 , 0.4 , 0.3 , 0.3 ,
0.8 , 0.4 , 0.6 , 0.66666667, 0.55555556]),
'Mean Validation Accuracy': 50.22222222222222,
'Validation Precision scores': array([0.5 , 0.6 , 0.42857143, 0.25 , 0.375 ,
1. , 0.44444444, 0.6 , 0.75 , 0.66666667]),
'Mean Validation Precision': 0.561468253968254,
'Validation Recall scores': array([0.33333333, 0.6 , 0.6 , 0.2 , 0.6 ,
0.6 , 0.8 , 0.6 , 0.6 , 0.4 ]),
'Mean Validation Recall': 0.5333333333333333,
'Validation F1 scores': array([0.4 , 0.6 , 0.5 , 0.22222222, 0.46153846,
0.75 , 0.57142857, 0.6 , 0.66666667, 0.5 ]),
'Mean Validation F1 Score': 0.5271855921855921}
model_name = "SVM"
plot_result(model_name,
"Accuracy",
"Accuracy scores in 10 Folds",
svm_result["Training Accuracy scores"],
svm_result["Validation Accuracy scores"],
num_folds=num_folds)
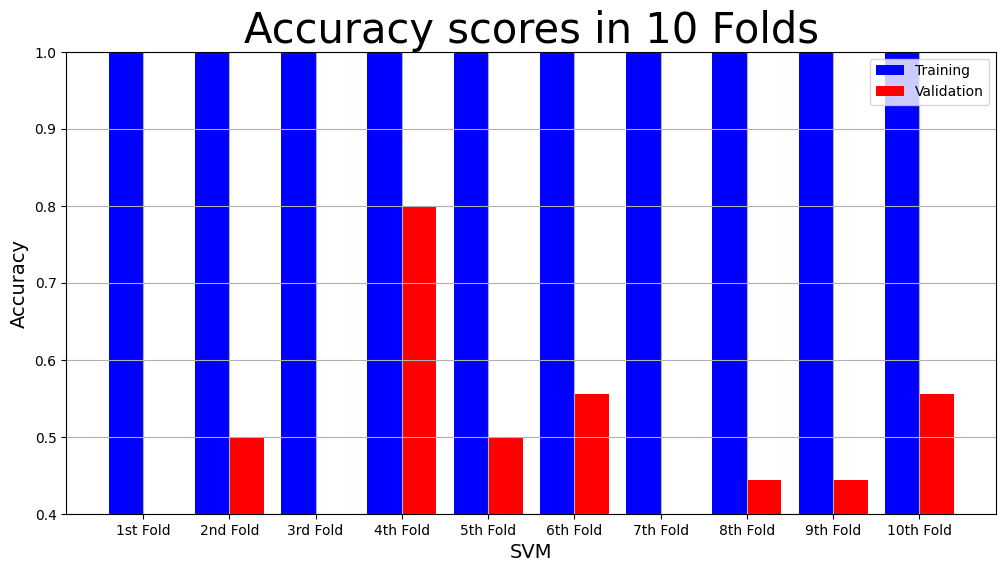
model_name = "SVM"
plot_result(model_name,
"F1",
"F1 scores in 10 Folds",
svm_result["Training F1 scores"],
svm_result["Validation F1 scores"],
num_folds=num_folds)
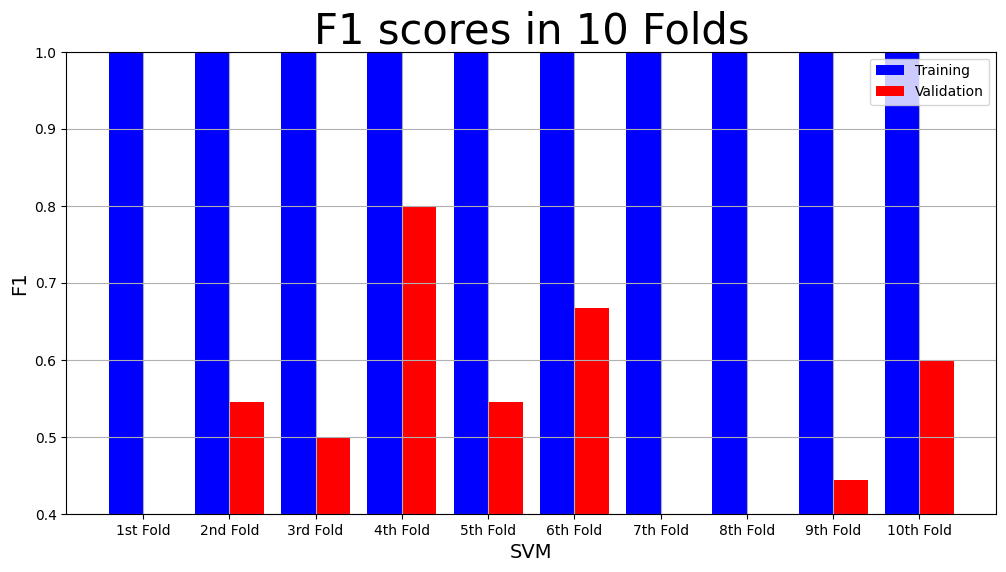
IES data#
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
#define the model
svm = LinearSVC(max_iter=50000)
#perform cross validation with model
svm_result_ies = cross_validation(svm, X_IES_ye, ies_y_E, num_folds)
svm_result_ies
{'Training Accuracy scores': array([0.62352941, 0.62352941, 0.61176471, 0.68235294, 0.57647059,
0.61627907, 0.63953488, 0.65116279, 0.60465116, 0.60465116]),
'Mean Training Accuracy': 62.33926128590971,
'Training Precision scores': array([0.60655738, 0.61290323, 0.61016949, 0.6557377 , 0.58064516,
0.6031746 , 0.62711864, 0.63333333, 0.59677419, 0.60344828]),
'Mean Training Precision': 0.61298620105756,
'Training Recall scores': array([0.82222222, 0.82608696, 0.7826087 , 0.86956522, 0.7826087 ,
0.82608696, 0.80434783, 0.82608696, 0.80434783, 0.76086957]),
'Mean Training Recall': 0.8104830917874397,
'Training F1 scores': array([0.69811321, 0.7037037 , 0.68571429, 0.74766355, 0.66666667,
0.69724771, 0.7047619 , 0.71698113, 0.68518519, 0.67307692]),
'Mean Training F1 Score': 0.6979114266555199,
'Validation Accuracy scores': array([0.6 , 0.6 , 0.3 , 0.3 , 0.7 ,
0.88888889, 0.66666667, 0.66666667, 0.88888889, 0.44444444]),
'Mean Validation Accuracy': 60.55555555555555,
'Validation Precision scores': array([0.75 , 0.57142857, 0.375 , 0.375 , 0.625 ,
1. , 0.625 , 0.625 , 0.83333333, 0.5 ]),
'Mean Validation Precision': 0.6279761904761905,
'Validation Recall scores': array([0.5, 0.8, 0.6, 0.6, 1. , 0.8, 1. , 1. , 1. , 0.6]),
'Mean Validation Recall': 0.7899999999999999,
'Validation F1 scores': array([0.6 , 0.66666667, 0.46153846, 0.46153846, 0.76923077,
0.88888889, 0.76923077, 0.76923077, 0.90909091, 0.54545455]),
'Mean Validation F1 Score': 0.6840870240870242}
print(f"The main results are \n Mean Validation F1: {svm_result_ies['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result_ies['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.6840870240870242
Mean Validation Accuracy 60.55555555555555
model_name = "SVM"
plot_result(model_name,
"F1",
"F1 scores in 10 Folds",
svm_result_ies["Training F1 scores"],
svm_result_ies["Validation F1 scores"],
num_folds=num_folds)
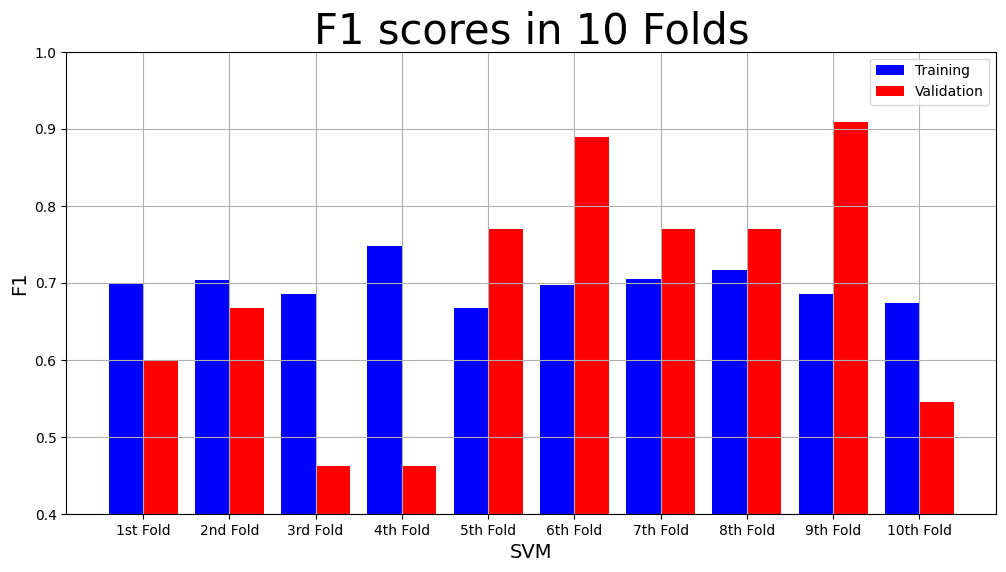
model_name = "SVM"
plot_result(model_name,
"Accuracy",
"Accuracy scores in 10 Folds",
svm_result_ies["Training Accuracy scores"],
svm_result_ies["Validation Accuracy scores"],
num_folds=num_folds)
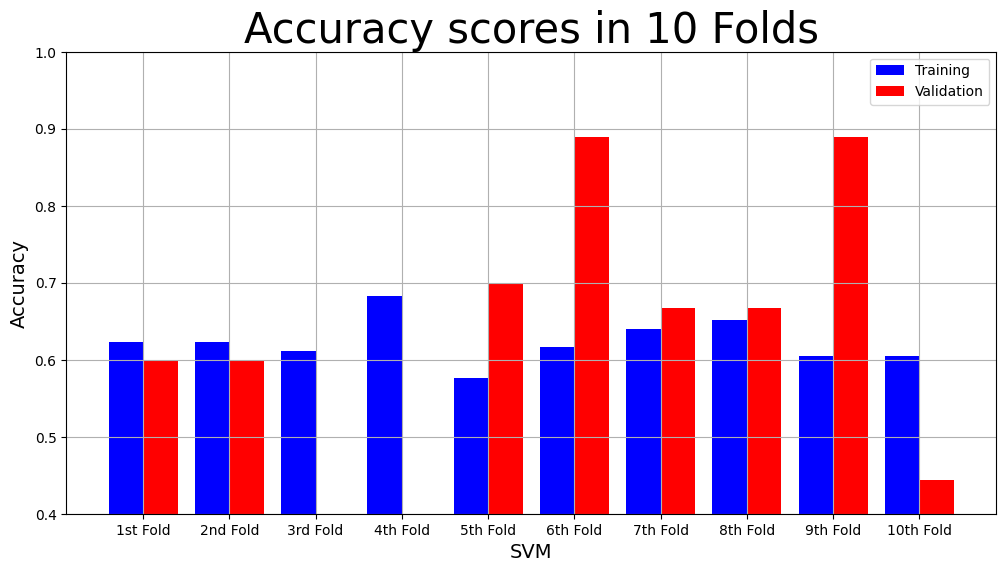
Let’s train an svm and see some predictions
svm.fit(X_IES_ye[:70], ies_y_E[:70])
LinearSVC(max_iter=50000)In a Jupyter environment, please rerun this cell to show the HTML representation or trust the notebook.
On GitHub, the HTML representation is unable to render, please try loading this page with nbviewer.org.
LinearSVC(max_iter=50000)
preds = svm.predict(X_IES_ye[70:])
preds
array([1, 1, 1, 1, 1, 1, 0, 0, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 1, 0, 1,
1, 1, 0])
ies_y_E[70:]
array([1, 1, 0, 1, 1, 0, 0, 0, 1, 1, 1, 1, 1, 1, 0, 0, 0, 0, 0, 1, 0, 1,
0, 1, 1])
np.mean(preds == ies_y_E[70:])
0.64
from sklearn.metrics import f1_score
f1_score(preds, ies_y_E[70:])
0.7096774193548386
We can see that using IES Data we get significantly better results than using BOLD data
Logistic Regression#
BOLD Data#
from sklearn.linear_model import LogisticRegression
#define the model
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_BOLD_ye, bold_y_E, num_folds)
logis_result
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.3 , 0.2 , 0.6 , 0.6 , 0.5 ,
0.55555556, 0.33333333, 0.55555556, 0.44444444, 0.55555556]),
'Mean Validation Accuracy': 46.444444444444436,
'Validation Precision scores': array([0.4 , 0.28571429, 0.57142857, 0.6 , 0.5 ,
0.57142857, 0.42857143, 0.66666667, 0.5 , 0.6 ]),
'Mean Validation Precision': 0.5123809523809524,
'Validation Recall scores': array([0.33333333, 0.4 , 0.8 , 0.6 , 0.6 ,
0.8 , 0.6 , 0.4 , 0.4 , 0.6 ]),
'Mean Validation Recall': 0.5533333333333333,
'Validation F1 scores': array([0.36363636, 0.33333333, 0.66666667, 0.6 , 0.54545455,
0.66666667, 0.5 , 0.5 , 0.44444444, 0.6 ]),
'Mean Validation F1 Score': 0.522020202020202}
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.522020202020202
Mean Validation Accuracy 46.444444444444436
model_name = "Logistic Regression"
plot_result(model_name,
"F1",
"F1 scores in 10 Folds",
logis_result["Training F1 scores"],
logis_result["Validation F1 scores"])
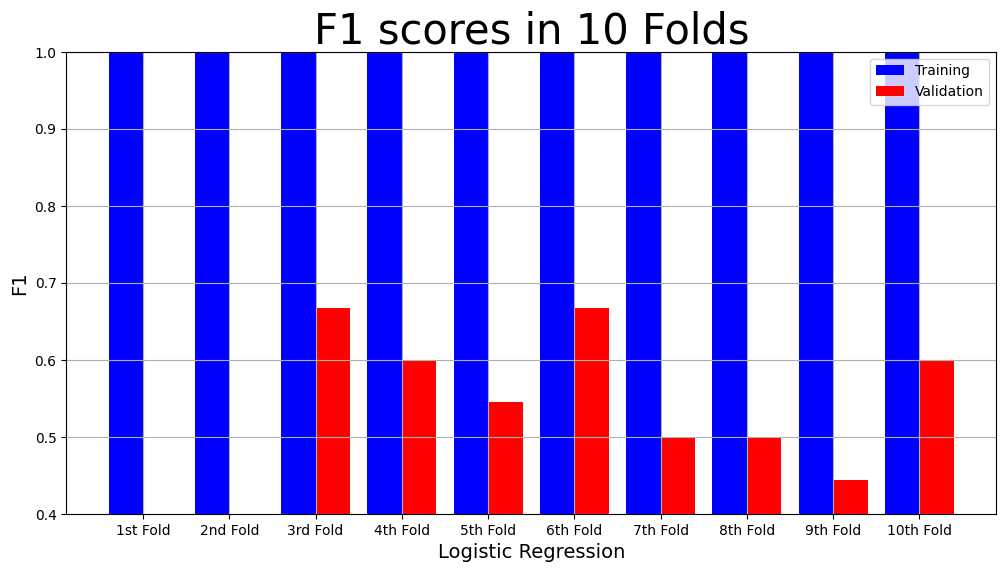
model_name = "Logistic Regression"
plot_result(model_name,
"Accuracy",
"Accuracy scores in 10 Folds",
logis_result["Training Accuracy scores"],
logis_result["Validation Accuracy scores"])
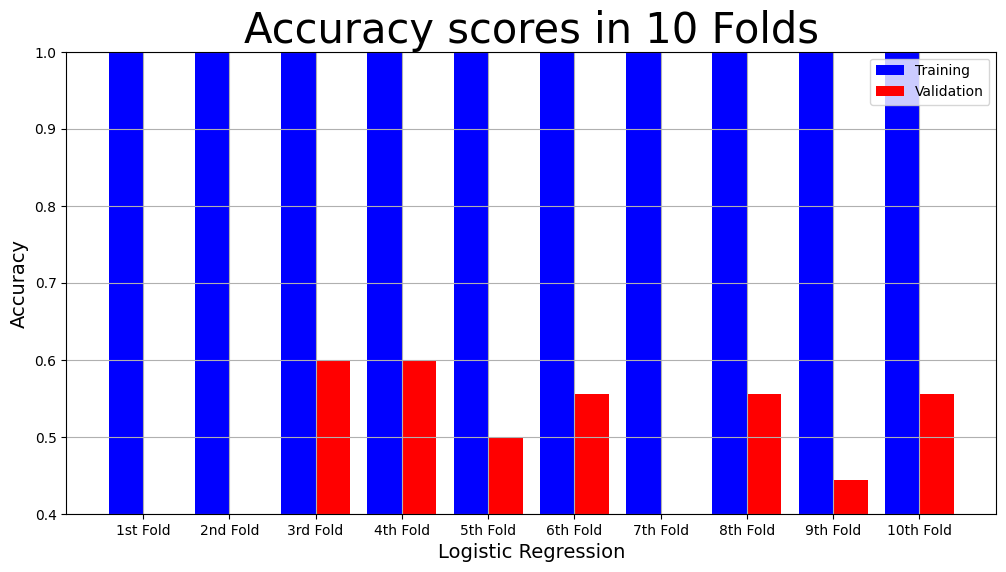
IES Data#
from sklearn.linear_model import LogisticRegression
#define the model
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES_ye, ies_y_E, num_folds)
logis_result
{'Training Accuracy scores': array([0.61176471, 0.61176471, 0.61176471, 0.69411765, 0.6 ,
0.61627907, 0.62790698, 0.61627907, 0.59302326, 0.62790698]),
'Mean Training Accuracy': 62.10807113543091,
'Training Precision scores': array([0.59677419, 0.61016949, 0.61016949, 0.66666667, 0.6 ,
0.61016949, 0.62068966, 0.61818182, 0.59016393, 0.62068966]),
'Mean Training Precision': 0.61436743977442,
'Training Recall scores': array([0.82222222, 0.7826087 , 0.7826087 , 0.86956522, 0.7826087 ,
0.7826087 , 0.7826087 , 0.73913043, 0.7826087 , 0.7826087 ]),
'Mean Training Recall': 0.7909178743961353,
'Training F1 scores': array([0.69158879, 0.68571429, 0.68571429, 0.75471698, 0.67924528,
0.68571429, 0.69230769, 0.67326733, 0.6728972 , 0.69230769]),
'Mean Training F1 Score': 0.691347381395027,
'Validation Accuracy scores': array([0.7 , 0.6 , 0.3 , 0.3 , 0.7 ,
0.77777778, 0.66666667, 0.55555556, 0.77777778, 0.55555556]),
'Mean Validation Accuracy': 59.33333333333333,
'Validation Precision scores': array([0.8 , 0.57142857, 0.375 , 0.375 , 0.625 ,
1. , 0.625 , 0.55555556, 0.8 , 0.6 ]),
'Mean Validation Precision': 0.6326984126984126,
'Validation Recall scores': array([0.66666667, 0.8 , 0.6 , 0.6 , 1. ,
0.6 , 1. , 1. , 0.8 , 0.6 ]),
'Mean Validation Recall': 0.7666666666666667,
'Validation F1 scores': array([0.72727273, 0.66666667, 0.46153846, 0.46153846, 0.76923077,
0.75 , 0.76923077, 0.71428571, 0.8 , 0.6 ]),
'Mean Validation F1 Score': 0.6719763569763569}
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.6719763569763569
Mean Validation Accuracy 59.33333333333333
model_name = "Logistic Regression"
plot_result(model_name,
"Accuracy",
"Accuracy scores in 10 Folds",
logis_result["Training Accuracy scores"],
logis_result["Validation Accuracy scores"])
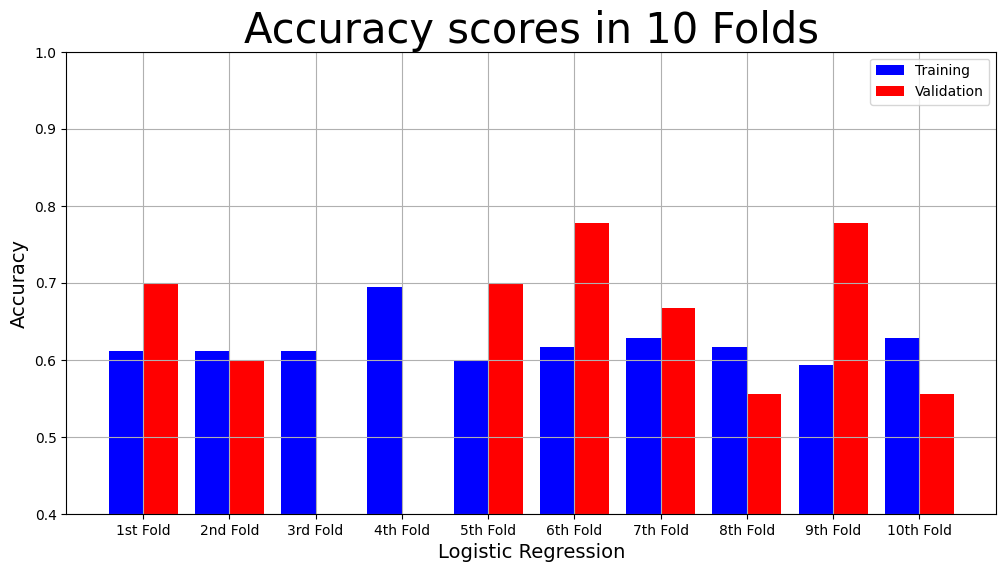
Multi-layer Perceptron (MLP)#
BOLD Data#
from sklearn.neural_network import MLPClassifier
# the input layer of the neural network has size 72 (the number of features)
# we reduce this to 50 and then to 30 and in the last layer, we return 2 values (the classes)
mlp = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=[50, 30]) # the solver is lbfgs because it works better than adam (the default one) for small datasets
mlp_result = cross_validation(mlp, X_BOLD_ye, bold_y_E, num_folds)
mlp_result
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.6 , 0.3 , 0.5 , 0.2 , 0.3 ,
0.66666667, 0.55555556, 0.55555556, 0.66666667, 0.66666667]),
'Mean Validation Accuracy': 50.11111111111111,
'Validation Precision scores': array([0.66666667, 0.375 , 0.5 , 0.28571429, 0.25 ,
0.75 , 0.66666667, 0.6 , 0.625 , 0.66666667]),
'Mean Validation Precision': 0.5385714285714285,
'Validation Recall scores': array([0.66666667, 0.6 , 1. , 0.4 , 0.2 ,
0.6 , 0.4 , 0.6 , 1. , 0.8 ]),
'Mean Validation Recall': 0.6266666666666667,
'Validation F1 scores': array([0.66666667, 0.46153846, 0.66666667, 0.33333333, 0.22222222,
0.66666667, 0.5 , 0.6 , 0.76923077, 0.72727273]),
'Mean Validation F1 Score': 0.5613597513597514}
print(f"The main results are \n Mean Validation F1: {mlp_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {mlp_result['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.5613597513597514
Mean Validation Accuracy 50.11111111111111
model_name = "MLP"
plot_result(model_name,
"F1",
"F1 scores in 10 Folds",
mlp_result["Training F1 scores"],
mlp_result["Validation F1 scores"])
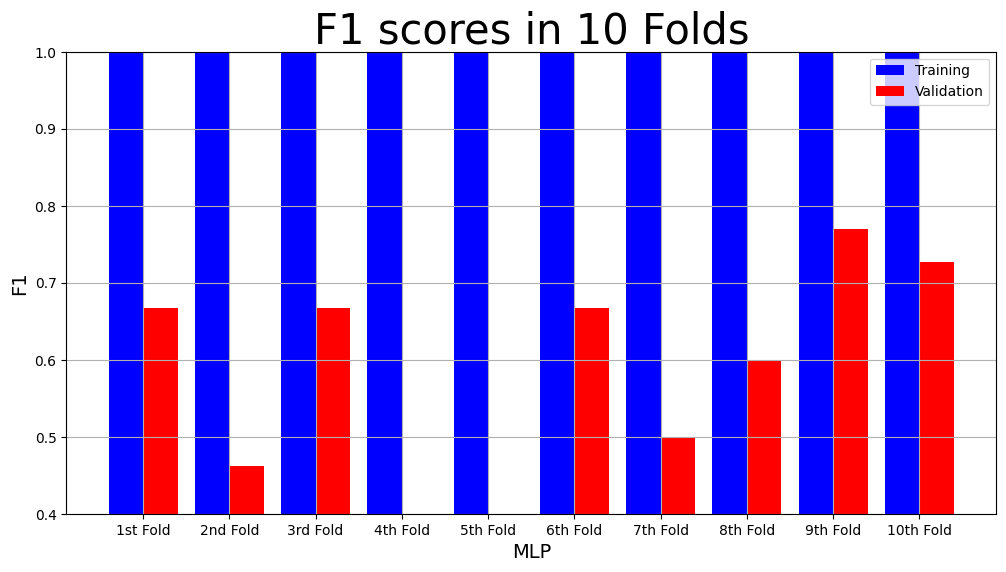
model_name = "MLP"
plot_result(model_name,
"Accuracy",
"Accuracy scores in 10 Folds",
mlp_result["Training Accuracy scores"],
mlp_result["Validation Accuracy scores"])
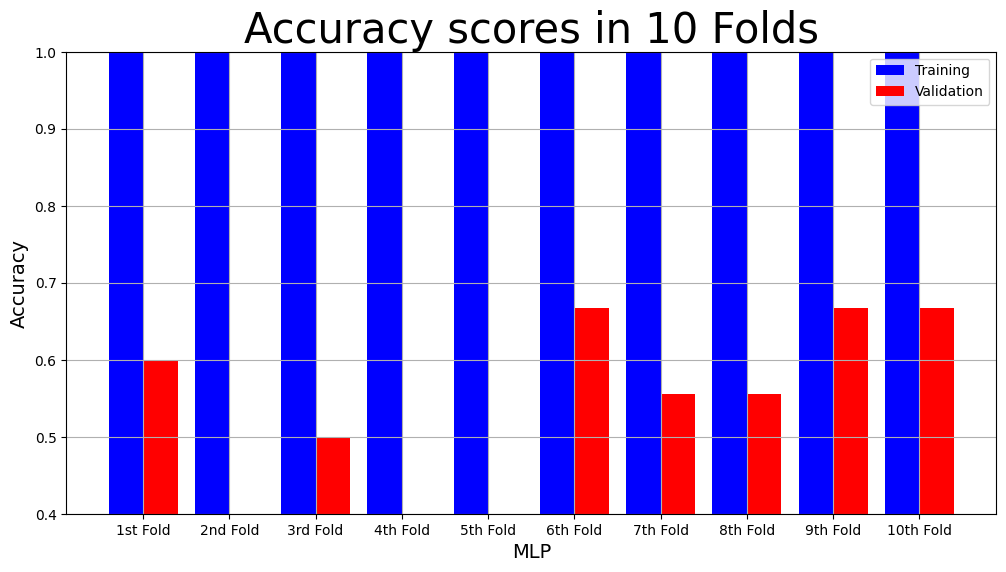
IES Data#
from sklearn.neural_network import MLPClassifier
# the input layer of the neural network has size 72 (the number of features)
# we reduce this to 50 and then to 30 and in the last layer, we return 2 values (the classes)
mlp = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=[50, 30], max_iter=5000) # the solver is lbfgs because it works better than adam (the default one) for small datasets
mlp_result = cross_validation(mlp, X_IES_ye, ies_y_E, num_folds)
mlp_result
{'Training Accuracy scores': array([0.90588235, 0.96470588, 1. , 0.98823529, 0.96470588,
1. , 0.97674419, 1. , 0.81395349, 0.97674419]),
'Mean Training Accuracy': 95.90971272229822,
'Training Precision scores': array([0.91111111, 0.95744681, 1. , 0.9787234 , 0.95744681,
1. , 0.95833333, 1. , 0.8 , 0.97826087]),
'Mean Training Precision': 0.9541322335286259,
'Training Recall scores': array([0.91111111, 0.97826087, 1. , 1. , 0.97826087,
1. , 1. , 1. , 0.86956522, 0.97826087]),
'Mean Training Recall': 0.9715458937198067,
'Training F1 scores': array([0.91111111, 0.96774194, 1. , 0.98924731, 0.96774194,
1. , 0.9787234 , 1. , 0.83333333, 0.97826087]),
'Mean Training F1 Score': 0.962615990106068,
'Validation Accuracy scores': array([0.4 , 0.4 , 0.4 , 0.5 , 0.2 ,
0.66666667, 0.55555556, 0.55555556, 0.44444444, 0.55555556]),
'Mean Validation Accuracy': 46.77777777777778,
'Validation Precision scores': array([0.5 , 0.42857143, 0.44444444, 0.5 , 0.2 ,
0.75 , 0.57142857, 0.6 , 0.5 , 0.57142857]),
'Mean Validation Precision': 0.5065873015873015,
'Validation Recall scores': array([0.16666667, 0.6 , 0.8 , 0.2 , 0.2 ,
0.6 , 0.8 , 0.6 , 0.4 , 0.8 ]),
'Mean Validation Recall': 0.5166666666666667,
'Validation F1 scores': array([0.25 , 0.5 , 0.57142857, 0.28571429, 0.2 ,
0.66666667, 0.66666667, 0.6 , 0.44444444, 0.66666667]),
'Mean Validation F1 Score': 0.48515873015873023}
print(f"The main results are \n Mean Validation F1: {mlp_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {mlp_result['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.48515873015873023
Mean Validation Accuracy 46.77777777777778
Conclusions from training to classify y_E#
Consistently across multiple models (SVM, logistic regression, and multi-layer perceptron), using IES Data yields better performance than BOLD data
SVM#
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
#define the model
svm = LinearSVC(max_iter=100000)
#perform cross validation with model
svm_result = cross_validation(svm, X_BOLD_yn, bold_y_N, num_folds)
svm_result
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.7 , 0.5 , 0.8 , 0.5 , 0.6 ,
0.44444444, 0.66666667, 0.44444444, 0.77777778, 0.22222222]),
'Mean Validation Accuracy': 56.55555555555555,
'Validation Precision scores': array([0.75 , 0.5 , 0.71428571, 0.5 , 0.57142857,
0.33333333, 1. , 0.5 , 1. , 0.25 ]),
'Mean Validation Precision': 0.6119047619047618,
'Validation Recall scores': array([0.6 , 0.4 , 1. , 0.6 , 0.8 , 0.25, 0.4 , 0.4 , 0.6 , 0.2 ]),
'Mean Validation Recall': 0.525,
'Validation F1 scores': array([0.66666667, 0.44444444, 0.83333333, 0.54545455, 0.66666667,
0.28571429, 0.57142857, 0.44444444, 0.75 , 0.22222222]),
'Mean Validation F1 Score': 0.543037518037518}
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.543037518037518
Mean Validation Accuracy 56.55555555555555
ies_y_N
array([0, 0, 0, 0, 1, 1, 1, 1, 1, 0, 1, 0, 0, 1, 1, 0, 1, 0, 1, 1, 1, 0,
0, 1, 1, 0, 1, 0, 0, 1, 1, 0, 0, 0, 0, 0, 1, 1, 0, 0, 1, 0, 1, 1,
1, 0, 0, 1, 0, 1, 1, 0, 1, 0, 1, 1, 1, 1, 0, 1, 0, 0, 1, 0, 1, 0,
0, 0, 1, 1, 0, 1, 1, 0, 1, 1, 1, 1, 1, 0, 0, 0, 1, 1, 0, 1, 0, 1,
1, 1, 0, 0, 0, 0, 0])
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
#define the model
svm = LinearSVC(max_iter=50000)
#perform cross validation with model
svm_result_ies = cross_validation(svm, X_IES_yn, ies_y_N, num_folds)
svm_result_ies
/usr/local/lib/python3.10/dist-packages/sklearn/metrics/_classification.py:1344: UndefinedMetricWarning: Precision is ill-defined and being set to 0.0 due to no predicted samples. Use `zero_division` parameter to control this behavior.
_warn_prf(average, modifier, msg_start, len(result))
{'Training Accuracy scores': array([0.61176471, 0.61176471, 0.58823529, 0.62352941, 0.57647059,
0.61627907, 0.60465116, 0.61627907, 0.6627907 , 0.60465116]),
'Mean Training Accuracy': 61.16415868673051,
'Training Precision scores': array([0.62790698, 0.62790698, 0.62162162, 0.63636364, 0.59090909,
0.64285714, 0.61904762, 0.62790698, 0.66666667, 0.60869565]),
'Mean Training Precision': 0.626988235987225,
'Training Recall scores': array([0.61363636, 0.61363636, 0.52272727, 0.63636364, 0.59090909,
0.6 , 0.59090909, 0.61363636, 0.68181818, 0.63636364]),
'Mean Training Recall': 0.6100000000000001,
'Training F1 scores': array([0.62068966, 0.62068966, 0.56790123, 0.63636364, 0.59090909,
0.62068966, 0.60465116, 0.62068966, 0.6741573 , 0.62222222]),
'Mean Training F1 Score': 0.6178963270913991,
'Validation Accuracy scores': array([0.4 , 0.6 , 0.4 , 0.6 , 0.5 ,
0.33333333, 0.66666667, 0.44444444, 0.33333333, 0.77777778]),
'Mean Validation Accuracy': 50.55555555555556,
'Validation Precision scores': array([0.4 , 0.6 , 0.33333333, 0.57142857, 0. ,
0.375 , 1. , 0.5 , 0.33333333, 0.8 ]),
'Mean Validation Precision': 0.4913095238095238,
'Validation Recall scores': array([0.4 , 0.6 , 0.2 , 0.8 , 0. , 0.75, 0.4 , 0.6 , 0.2 , 0.8 ]),
'Mean Validation Recall': 0.475,
'Validation F1 scores': array([0.4 , 0.6 , 0.25 , 0.66666667, 0. ,
0.5 , 0.57142857, 0.54545455, 0.25 , 0.8 ]),
'Mean Validation F1 Score': 0.4583549783549784}
print(f"The main results are \n Mean Validation F1: {svm_result_ies['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result_ies['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.4583549783549784
Mean Validation Accuracy 50.55555555555556
Logistic Regression#
from sklearn.linear_model import LogisticRegression
#define the model
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_BOLD_yn, bold_y_N, num_folds)
logis_result
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.7 , 0.5 , 0.8 , 0.5 , 0.6 ,
0.44444444, 0.88888889, 0.44444444, 0.88888889, 0.33333333]),
'Mean Validation Accuracy': 60.999999999999986,
'Validation Precision scores': array([0.75 , 0.5 , 0.71428571, 0.5 , 0.57142857,
0. , 1. , 0.5 , 1. , 0.4 ]),
'Mean Validation Precision': 0.5935714285714286,
'Validation Recall scores': array([0.6, 0.4, 1. , 0.6, 0.8, 0. , 0.8, 0.4, 0.8, 0.4]),
'Mean Validation Recall': 0.58,
'Validation F1 scores': array([0.66666667, 0.44444444, 0.83333333, 0.54545455, 0.66666667,
0. , 0.88888889, 0.44444444, 0.88888889, 0.4 ]),
'Mean Validation F1 Score': 0.5778787878787879}
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.5778787878787879
Mean Validation Accuracy 60.999999999999986
from sklearn.linear_model import LogisticRegression
#define the model
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_IES_ye, ies_y_E, num_folds)
logis_result
{'Training Accuracy scores': array([0.61176471, 0.61176471, 0.61176471, 0.69411765, 0.6 ,
0.61627907, 0.62790698, 0.61627907, 0.59302326, 0.62790698]),
'Mean Training Accuracy': 62.10807113543091,
'Training Precision scores': array([0.59677419, 0.61016949, 0.61016949, 0.66666667, 0.6 ,
0.61016949, 0.62068966, 0.61818182, 0.59016393, 0.62068966]),
'Mean Training Precision': 0.61436743977442,
'Training Recall scores': array([0.82222222, 0.7826087 , 0.7826087 , 0.86956522, 0.7826087 ,
0.7826087 , 0.7826087 , 0.73913043, 0.7826087 , 0.7826087 ]),
'Mean Training Recall': 0.7909178743961353,
'Training F1 scores': array([0.69158879, 0.68571429, 0.68571429, 0.75471698, 0.67924528,
0.68571429, 0.69230769, 0.67326733, 0.6728972 , 0.69230769]),
'Mean Training F1 Score': 0.691347381395027,
'Validation Accuracy scores': array([0.7 , 0.6 , 0.3 , 0.3 , 0.7 ,
0.77777778, 0.66666667, 0.55555556, 0.77777778, 0.55555556]),
'Mean Validation Accuracy': 59.33333333333333,
'Validation Precision scores': array([0.8 , 0.57142857, 0.375 , 0.375 , 0.625 ,
1. , 0.625 , 0.55555556, 0.8 , 0.6 ]),
'Mean Validation Precision': 0.6326984126984126,
'Validation Recall scores': array([0.66666667, 0.8 , 0.6 , 0.6 , 1. ,
0.6 , 1. , 1. , 0.8 , 0.6 ]),
'Mean Validation Recall': 0.7666666666666667,
'Validation F1 scores': array([0.72727273, 0.66666667, 0.46153846, 0.46153846, 0.76923077,
0.75 , 0.76923077, 0.71428571, 0.8 , 0.6 ]),
'Mean Validation F1 Score': 0.6719763569763569}
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.6719763569763569
Mean Validation Accuracy 59.33333333333333
MLP#
from sklearn.neural_network import MLPClassifier
# the input layer of the neural network has size 72 (the number of features)
# we reduce this to 50 and then to 30 and in the last layer, we return 2 values (the classes)
mlp = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=[50, 30]) # the solver is lbfgs because it works better than adam (the default one) for small datasets
mlp_result = cross_validation(mlp, X_BOLD_yn, bold_y_N, num_folds)
mlp_result
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.6 , 0.6 , 0.6 , 0.6 , 0.5 ,
0.44444444, 0.66666667, 0.66666667, 0.33333333, 0.22222222]),
'Mean Validation Accuracy': 52.33333333333332,
'Validation Precision scores': array([0.66666667, 0.57142857, 0.6 , 0.57142857, 0.5 ,
0. , 1. , 0.66666667, 0.33333333, 0.33333333]),
'Mean Validation Precision': 0.5242857142857142,
'Validation Recall scores': array([0.4, 0.8, 0.6, 0.8, 0.4, 0. , 0.4, 0.8, 0.2, 0.4]),
'Mean Validation Recall': 0.4800000000000001,
'Validation F1 scores': array([0.5 , 0.66666667, 0.6 , 0.66666667, 0.44444444,
0. , 0.57142857, 0.72727273, 0.25 , 0.36363636]),
'Mean Validation F1 Score': 0.47901154401154394}
print(f"The main results are \n Mean Validation F1: {mlp_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {mlp_result['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.47901154401154394
Mean Validation Accuracy 52.33333333333332
from sklearn.neural_network import MLPClassifier
# the input layer of the neural network has size 72 (the number of features)
# we reduce this to 50 and then to 30 and in the last layer, we return 2 values (the classes)
mlp = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=[50, 30], max_iter=5000) # the solver is lbfgs because it works better than adam (the default one) for small datasets
mlp_result_ies = cross_validation(mlp, X_IES_yn, ies_y_N, num_folds)
mlp_result_ies
{'Training Accuracy scores': array([0.90588235, 1. , 0.82352941, 0.92941176, 1. ,
0.89534884, 0.90697674, 0.93023256, 0.98837209, 0.98837209]),
'Mean Training Accuracy': 93.6812585499316,
'Training Precision scores': array([0.89130435, 1. , 0.82222222, 0.93181818, 1. ,
0.84615385, 0.90909091, 0.93181818, 1. , 1. ]),
'Mean Training Precision': 0.9332407688929429,
'Training Recall scores': array([0.93181818, 1. , 0.84090909, 0.93181818, 1. ,
0.97777778, 0.90909091, 0.93181818, 0.97727273, 0.97727273]),
'Mean Training Recall': 0.9477777777777776,
'Training F1 scores': array([0.91111111, 1. , 0.83146067, 0.93181818, 1. ,
0.90721649, 0.90909091, 0.93181818, 0.98850575, 0.98850575]),
'Mean Training F1 Score': 0.9399527047093923,
'Validation Accuracy scores': array([0.6 , 0.6 , 0.6 , 0.7 , 0.3 ,
0.55555556, 0.44444444, 0.44444444, 0.22222222, 0.55555556]),
'Mean Validation Accuracy': 50.22222222222222,
'Validation Precision scores': array([0.55555556, 0.6 , 0.57142857, 0.66666667, 0.25 ,
0.5 , 0.5 , 0.5 , 0.25 , 0.66666667]),
'Mean Validation Precision': 0.506031746031746,
'Validation Recall scores': array([1. , 0.6, 0.8, 0.8, 0.2, 0.5, 0.4, 0.6, 0.2, 0.4]),
'Mean Validation Recall': 0.55,
'Validation F1 scores': array([0.71428571, 0.6 , 0.66666667, 0.72727273, 0.22222222,
0.5 , 0.44444444, 0.54545455, 0.22222222, 0.5 ]),
'Mean Validation F1 Score': 0.5142568542568543}
print(f"The main results are \n Mean Validation F1: {mlp_result_ies['Mean Validation F1 Score']} \n Mean Validation Accuracy {mlp_result_ies['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.5142568542568543
Mean Validation Accuracy 50.22222222222222
Conclusion#
BOLD data seems to be a bit better than IES Data to predict y_N
Training Y_A#
SVM#
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
#define the model
svm = LinearSVC(max_iter=1000000)
#perform cross validation with model
svm_result = cross_validation(svm, X_BOLD_ya, bold_y_A, num_folds)
svm_result
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.84615385, 0.53846154, 0.76923077, 1. , 0.46153846,
0.76923077, 0.61538462, 0.91666667, 0.75 , 0.91666667]),
'Mean Validation Accuracy': 75.83333333333333,
'Validation Precision scores': array([0.77777778, 1. , 0.75 , 1. , 0.5 ,
1. , 1. , 1. , 0.71428571, 1. ]),
'Mean Validation Precision': 0.8742063492063492,
'Validation Recall scores': array([1. , 0.14285714, 0.85714286, 1. , 0.28571429,
0.57142857, 0.28571429, 0.83333333, 0.83333333, 0.83333333]),
'Mean Validation Recall': 0.6642857142857143,
'Validation F1 scores': array([0.875 , 0.25 , 0.8 , 1. , 0.36363636,
0.72727273, 0.44444444, 0.90909091, 0.76923077, 0.90909091]),
'Mean Validation F1 Score': 0.7047766122766123}
print(f"The main results are \n Mean Validation F1: {svm_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.7047766122766123
Mean Validation Accuracy 75.83333333333333
from sklearn.linear_model import LogisticRegression
from sklearn.svm import LinearSVC
#define the model
svm = LinearSVC(max_iter=1000000)
#perform cross validation with model
svm_result_ies = cross_validation(svm, X_IES_ya, ies_y_A, num_folds)
svm_result_ies
{'Training Accuracy scores': array([0.61403509, 0.68421053, 0.62280702, 0.61403509, 0.65789474,
0.6754386 , 0.65789474, 0.70434783, 0.66086957, 0.68695652]),
'Mean Training Accuracy': 65.78489702517162,
'Training Precision scores': array([0.6 , 0.69354839, 0.62686567, 0.61111111, 0.65671642,
0.65333333, 0.65217391, 0.67532468, 0.6375 , 0.67123288]),
'Mean Training Precision': 0.647780638617394,
'Training Recall scores': array([0.8 , 0.71666667, 0.7 , 0.73333333, 0.73333333,
0.81666667, 0.75 , 0.85245902, 0.83606557, 0.80327869]),
'Mean Training Recall': 0.7741803278688525,
'Training F1 scores': array([0.68571429, 0.70491803, 0.66141732, 0.66666667, 0.69291339,
0.72592593, 0.69767442, 0.75362319, 0.72340426, 0.73134328]),
'Mean Training F1 Score': 0.7043600765666869,
'Validation Accuracy scores': array([0.84615385, 0.23076923, 0.38461538, 0.76923077, 0.61538462,
0.84615385, 0.69230769, 0.58333333, 0.66666667, 0.41666667]),
'Mean Validation Accuracy': 60.51282051282052,
'Validation Precision scores': array([0.77777778, 0.28571429, 0.4 , 0.75 , 0.625 ,
1. , 0.63636364, 0.57142857, 0.625 , 0.42857143]),
'Mean Validation Precision': 0.6099855699855701,
'Validation Recall scores': array([1. , 0.28571429, 0.28571429, 0.85714286, 0.71428571,
0.71428571, 1. , 0.66666667, 0.83333333, 0.5 ]),
'Mean Validation Recall': 0.6857142857142857,
'Validation F1 scores': array([0.875 , 0.28571429, 0.33333333, 0.8 , 0.66666667,
0.83333333, 0.77777778, 0.61538462, 0.71428571, 0.46153846]),
'Mean Validation F1 Score': 0.6363034188034189}
print(f"The main results are \n Mean Validation F1: {svm_result_ies['Mean Validation F1 Score']} \n Mean Validation Accuracy {svm_result_ies['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.6363034188034189
Mean Validation Accuracy 60.51282051282052
Logistic Regression#
from sklearn.linear_model import LogisticRegression
#define the model
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result = cross_validation(logis_reg_model, X_BOLD_ya, bold_y_A, num_folds)
logis_result
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.84615385, 0.53846154, 0.69230769, 0.92307692, 0.69230769,
0.84615385, 0.69230769, 0.75 , 0.75 , 0.91666667]),
'Mean Validation Accuracy': 76.47435897435898,
'Validation Precision scores': array([0.77777778, 1. , 0.71428571, 1. , 0.71428571,
1. , 1. , 1. , 0.71428571, 1. ]),
'Mean Validation Precision': 0.8920634920634921,
'Validation Recall scores': array([1. , 0.14285714, 0.71428571, 0.85714286, 0.71428571,
0.71428571, 0.42857143, 0.5 , 0.83333333, 0.83333333]),
'Mean Validation Recall': 0.6738095238095237,
'Validation F1 scores': array([0.875 , 0.25 , 0.71428571, 0.92307692, 0.71428571,
0.83333333, 0.6 , 0.66666667, 0.76923077, 0.90909091]),
'Mean Validation F1 Score': 0.725497002997003}
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.725497002997003
Mean Validation Accuracy 76.47435897435898
from sklearn.linear_model import LogisticRegression
#define the model
logis_reg_model = LogisticRegression(penalty='l2', max_iter=10000)
#perform cross validation with model
logis_result_ies = cross_validation(logis_reg_model, X_IES_ye, ies_y_E, num_folds)
logis_result_ies
{'Training Accuracy scores': array([0.61176471, 0.61176471, 0.61176471, 0.69411765, 0.6 ,
0.61627907, 0.62790698, 0.61627907, 0.59302326, 0.62790698]),
'Mean Training Accuracy': 62.10807113543091,
'Training Precision scores': array([0.59677419, 0.61016949, 0.61016949, 0.66666667, 0.6 ,
0.61016949, 0.62068966, 0.61818182, 0.59016393, 0.62068966]),
'Mean Training Precision': 0.61436743977442,
'Training Recall scores': array([0.82222222, 0.7826087 , 0.7826087 , 0.86956522, 0.7826087 ,
0.7826087 , 0.7826087 , 0.73913043, 0.7826087 , 0.7826087 ]),
'Mean Training Recall': 0.7909178743961353,
'Training F1 scores': array([0.69158879, 0.68571429, 0.68571429, 0.75471698, 0.67924528,
0.68571429, 0.69230769, 0.67326733, 0.6728972 , 0.69230769]),
'Mean Training F1 Score': 0.691347381395027,
'Validation Accuracy scores': array([0.7 , 0.6 , 0.3 , 0.3 , 0.7 ,
0.77777778, 0.66666667, 0.55555556, 0.77777778, 0.55555556]),
'Mean Validation Accuracy': 59.33333333333333,
'Validation Precision scores': array([0.8 , 0.57142857, 0.375 , 0.375 , 0.625 ,
1. , 0.625 , 0.55555556, 0.8 , 0.6 ]),
'Mean Validation Precision': 0.6326984126984126,
'Validation Recall scores': array([0.66666667, 0.8 , 0.6 , 0.6 , 1. ,
0.6 , 1. , 1. , 0.8 , 0.6 ]),
'Mean Validation Recall': 0.7666666666666667,
'Validation F1 scores': array([0.72727273, 0.66666667, 0.46153846, 0.46153846, 0.76923077,
0.75 , 0.76923077, 0.71428571, 0.8 , 0.6 ]),
'Mean Validation F1 Score': 0.6719763569763569}
print(f"The main results are \n Mean Validation F1: {logis_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {logis_result_ies['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.6719763569763569
Mean Validation Accuracy 59.33333333333333
MLP#
from sklearn.neural_network import MLPClassifier
# the input layer of the neural network has size 72 (the number of features)
# we reduce this to 50 and then to 30 and in the last layer, we return 2 values (the classes)
mlp = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=[50, 30]) # the solver is lbfgs because it works better than adam (the default one) for small datasets
mlp_result = cross_validation(mlp, X_BOLD_ya, bold_y_A, num_folds)
mlp_result
{'Training Accuracy scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Accuracy': 100.0,
'Training Precision scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Precision': 1.0,
'Training Recall scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training Recall': 1.0,
'Training F1 scores': array([1., 1., 1., 1., 1., 1., 1., 1., 1., 1.]),
'Mean Training F1 Score': 1.0,
'Validation Accuracy scores': array([0.69230769, 1. , 0.61538462, 0.84615385, 0.53846154,
0.84615385, 0.84615385, 0.83333333, 0.75 , 1. ]),
'Mean Validation Accuracy': 79.67948717948718,
'Validation Precision scores': array([0.71428571, 1. , 0.6 , 1. , 0.6 ,
1. , 1. , 1. , 0.71428571, 1. ]),
'Mean Validation Precision': 0.862857142857143,
'Validation Recall scores': array([0.71428571, 1. , 0.85714286, 0.71428571, 0.42857143,
0.71428571, 0.71428571, 0.66666667, 0.83333333, 1. ]),
'Mean Validation Recall': 0.7642857142857142,
'Validation F1 scores': array([0.71428571, 1. , 0.70588235, 0.83333333, 0.5 ,
0.83333333, 0.83333333, 0.8 , 0.76923077, 1. ]),
'Mean Validation F1 Score': 0.798939883645766}
print(f"The main results are \n Mean Validation F1: {mlp_result['Mean Validation F1 Score']} \n Mean Validation Accuracy {mlp_result['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.798939883645766
Mean Validation Accuracy 79.67948717948718
from sklearn.neural_network import MLPClassifier
# the input layer of the neural network has size 72 (the number of features)
# we reduce this to 50 and then to 30 and in the last layer, we return 2 values (the classes)
mlp = MLPClassifier(solver='lbfgs', alpha=1e-5, hidden_layer_sizes=[50, 30], max_iter=5000) # the solver is lbfgs because it works better than adam (the default one) for small datasets
mlp_result_ies = cross_validation(mlp, X_IES_ya, ies_y_A, num_folds)
mlp_result_ies
{'Training Accuracy scores': array([1. , 1. , 0.96491228, 0.87719298, 0.92982456,
1. , 1. , 0.9826087 , 1. , 1. ]),
'Mean Training Accuracy': 97.54538520213578,
'Training Precision scores': array([1. , 1. , 0.98275862, 0.91071429, 0.94827586,
1. , 1. , 0.98360656, 1. , 1. ]),
'Mean Training Precision': 0.9825355325849955,
'Training Recall scores': array([1. , 1. , 0.95 , 0.85 , 0.91666667,
1. , 1. , 0.98360656, 1. , 1. ]),
'Mean Training Recall': 0.9700273224043716,
'Training F1 scores': array([1. , 1. , 0.96610169, 0.87931034, 0.93220339,
1. , 1. , 0.98360656, 1. , 1. ]),
'Mean Training F1 Score': 0.9761221986950398,
'Validation Accuracy scores': array([0.92307692, 0.92307692, 0.84615385, 0.69230769, 0.69230769,
0.76923077, 0.76923077, 0.83333333, 0.91666667, 0.91666667]),
'Mean Validation Accuracy': 82.82051282051283,
'Validation Precision scores': array([1. , 1. , 0.85714286, 0.8 , 0.8 ,
1. , 1. , 0.83333333, 1. , 1. ]),
'Mean Validation Precision': 0.9290476190476191,
'Validation Recall scores': array([0.85714286, 0.85714286, 0.85714286, 0.57142857, 0.57142857,
0.57142857, 0.57142857, 0.83333333, 0.83333333, 0.83333333]),
'Mean Validation Recall': 0.7357142857142855,
'Validation F1 scores': array([0.92307692, 0.92307692, 0.85714286, 0.66666667, 0.66666667,
0.72727273, 0.72727273, 0.83333333, 0.90909091, 0.90909091]),
'Mean Validation F1 Score': 0.8142690642690642}
print(f"The main results are \n Mean Validation F1: {mlp_result_ies['Mean Validation F1 Score']} \n Mean Validation Accuracy {mlp_result_ies['Mean Validation Accuracy']}")
The main results are
Mean Validation F1: 0.8142690642690642
Mean Validation Accuracy 82.82051282051283
Conclusion#
Using SVM and logistic regression, BOLD data is better than IES to predict Y_A. However, using MLP is able to give better results using IES than BOLD to predict Y_A.
OLD CODE
# Plot F1-Score Result
plot_result(model_name,
"F1",
"F1 Scores in 10 Folds",
decision_tree_result["Training F1 scores"],
decision_tree_result["Validation F1 scores"])
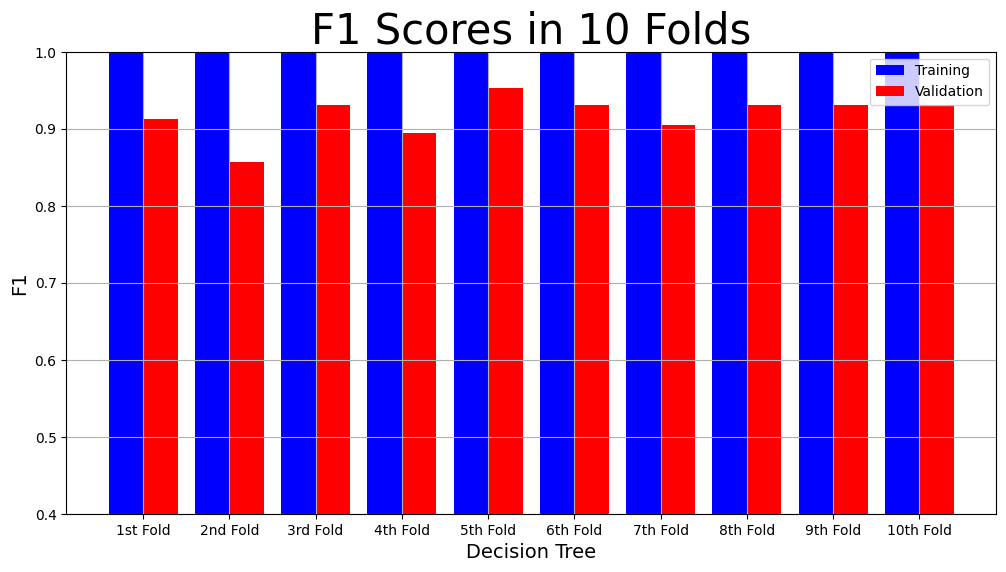
The visualizations show that the training accuracy, precision, recall, and f1 scores in each fold are 100%. But the validation accuracy, precision, recall and f1 scores are not as high. We call this over-fitting. The model performs admirably on the training data. But not so much on the validation set.
##Increase Parameter to combat Over-fitting
Visualizing your results like this can help you see if your model is over-fitting. We adjust the min_samples_split hyper-parameter in the decision tree algorithm. It will fix the over-fitting problem. The default value of the min_samples_split parameter is 2. We increase the value to 5.
decision_tree_model_2 = DecisionTreeClassifier(criterion="entropy",
min_samples_split=5,
random_state=0)
decision_tree_result_2 = cross_validation(decision_tree_model_2, X, encoded_y, 10) #specify 10 cross validation here
print(decision_tree_result_2)
{'Training Accuracy scores': array([0.99804688, 0.99804688, 0.99609375, 0.99609375, 0.99414062,
0.9921875 , 0.99414062, 0.99609375, 0.99414062, 0.99220273]), 'Mean Training Accuracy': 99.51187104044834, 'Training Precision scores': array([0.9947644 , 1. , 1. , 0.98963731, 0.99473684,
0.99470899, 1. , 1. , 0.99473684, 0.99470899]), 'Mean Training Precision': 0.9963293377233757, 'Training Recall scores': array([1. , 0.99473684, 0.9895288 , 1. , 0.9895288 ,
0.98429319, 0.98429319, 0.9895288 , 0.9895288 , 0.98429319]), 'Mean Training Recall': 0.9905731606503169, 'Training F1 scores': array([0.99737533, 0.99736148, 0.99473684, 0.99479167, 0.99212598,
0.98947368, 0.99208443, 0.99473684, 0.99212598, 0.98947368]), 'Mean Training F1 Score': 0.9934285926176409, 'Validation Accuracy scores': array([0.92982456, 0.84210526, 0.96491228, 0.9122807 , 0.98245614,
0.94736842, 0.9122807 , 0.94736842, 0.96491228, 0.96428571]), 'Mean Validation Accuracy': 93.6779448621554, 'Validation Precision scores': array([0.875 , 0.84210526, 0.95238095, 0.94444444, 1. ,
0.90909091, 0.9 , 0.90909091, 0.91304348, 0.91304348]), 'Mean Validation Precision': 0.9158199434686848, 'Validation Recall scores': array([0.95454545, 0.72727273, 0.95238095, 0.80952381, 0.95238095,
0.95238095, 0.85714286, 0.95238095, 1. , 1. ]), 'Mean Validation Recall': 0.9158008658008658, 'Validation F1 scores': array([0.91304348, 0.7804878 , 0.95238095, 0.87179487, 0.97560976,
0.93023256, 0.87804878, 0.93023256, 0.95454545, 0.95454545]), 'Mean Validation F1 Score': 0.9140921669270087}
# Plot Accuracy Result
plot_result(model_name,
"Accuracy",
"Accuracy scores in 10 Folds",
decision_tree_result_2["Training Accuracy scores"],
decision_tree_result_2["Validation Accuracy scores"])
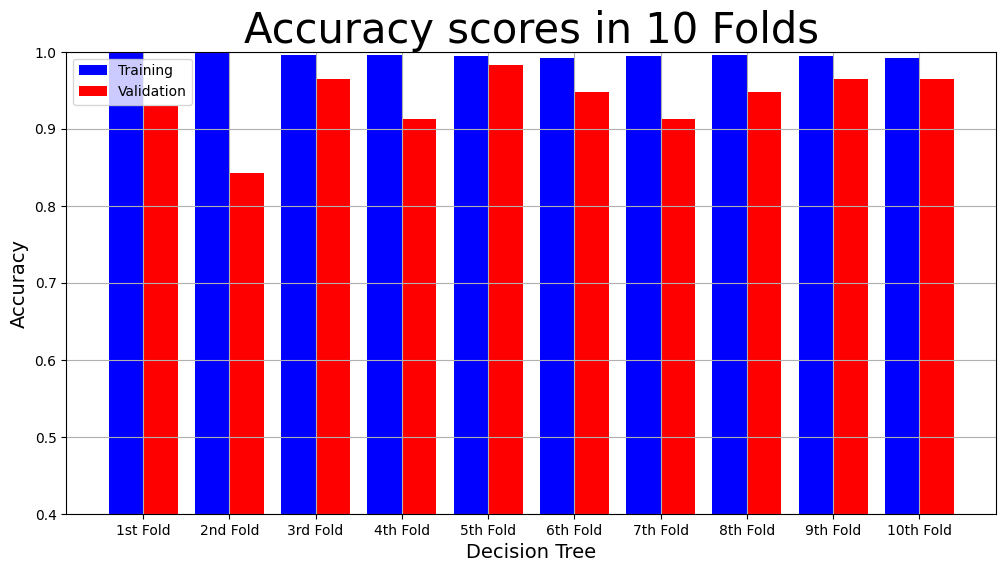
# Plot Precision Result
plot_result(model_name,
"Precision",
"Precision scores in 10 Folds",
decision_tree_result_2["Training Precision scores"],
decision_tree_result_2["Validation Precision scores"])
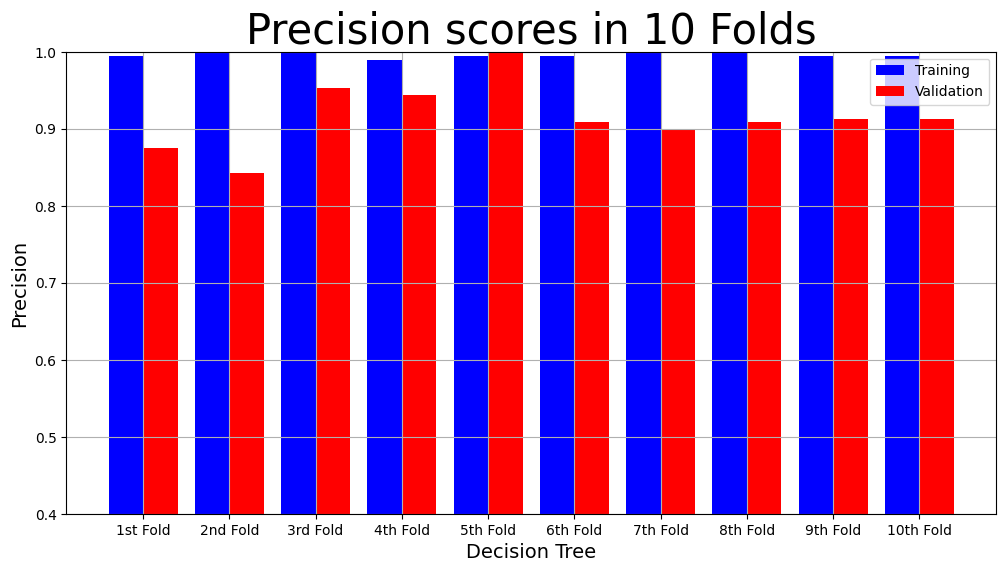
# Plot Recall Result
plot_result(model_name,
"Recall",
"Recall scores in 10 Folds",
decision_tree_result_2["Training Recall scores"],
decision_tree_result_2["Validation Recall scores"])
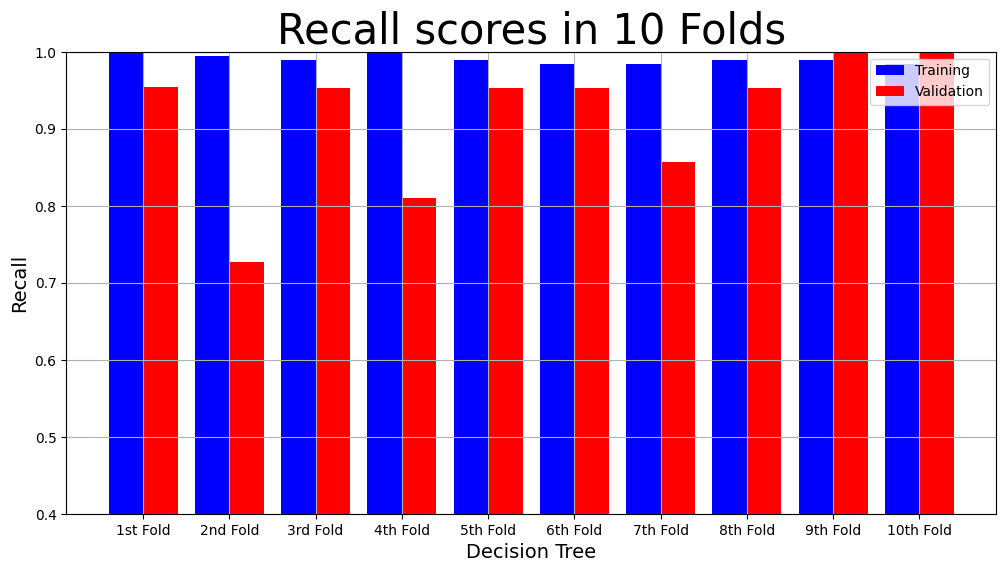
# Plot F1-Score Result
plot_result(model_name,
"F1",
"F1 Scores in 10 Folds",
decision_tree_result_2["Training F1 scores"],
decision_tree_result_2["Validation F1 scores"])